Investing in Student Housing in Ames, Iowa
Introduction
College towns are known to offer safe, recession-prone, high-return investment opportunities. The case study of Ames, Iowa, home of Iowa State University, is intended to generate insights generalizable to other student towns. Given potential properties for which an investor can make an offer, what offer shall be made? In addition, given that offer, what returns can be expected?
To answer the first question, I develop a predictive machine learning model that would allow an investor to learn the market value of a property. In the process, I also develop slightly less accurate but more generalizable and interpretable models, thus training a spectrum of models from highly accurate/less interpretable to less accurate/highly interpretable. These models provide a better understanding of the problem and can be used to easily replace the model deployed if having a highly interpretable model becomes paramount to the stakeholders.
To answer the second question, I construct a histogram of expected returns measured by cap rates. The cap rates distribution in this histogram roughly matches the market estimates. In addition, I build and deploy a Streamlit/Heroku app to enable an investor to contact the current home owner. This app shows locations, information on property and owner, projected price, and expected returns for a representative sample of properties. It can be easily generalized to cover all of the properties in the data or new data previously unseen by the models.
Data Preparation and Model Training
Please skip to the next section unless interested in the machine learning side of the project
Data and Data Preprocessing
The data available on Kaggle consists of about 2850 non-duplicate observations of house features and prices gathered from 2006 to 2010. The features are a standard set of 80, including living area, house quality, neighborhood, and basement quality (an asset in a town located along the Tornado Belt). While the date range included the 2008 recession, the house prices in Ames and other rural US areas were relatively unaffected by it.
Given the large number of available features, and an observation that engineering additional features from the ones already in the model was not found helpful in previous work, I decide to forego creating more features from the existing ones. However, I add the house address and owner data, merge in latitudes and longitudes using Nominatim API, and derive a feature indicating distance to Iowa State University. The latitude and longitude increase predictive accuracy, and, together with distance to Iowa State University, are critical for building the Ames Housing App.
In addition, many of the features have skewed distributions, which would influence distance-based machine learning models. For example, observe the long tails in the box plots of some of the square footage columns.

If my primary goal were to further improve the linear regression model discussed in this blog post, I would take more care to transform some of these features. I would apply the necessary box-cox or log transforms, discard a feature having a hard-to-tame distribution if a correlated but better distributed feature is available, etc. Since I rely mostly on tree-based models, this aspect is less critical. However, the residuals would likely 'fan out' if a log transform is not applied to price, as the graphs below show.
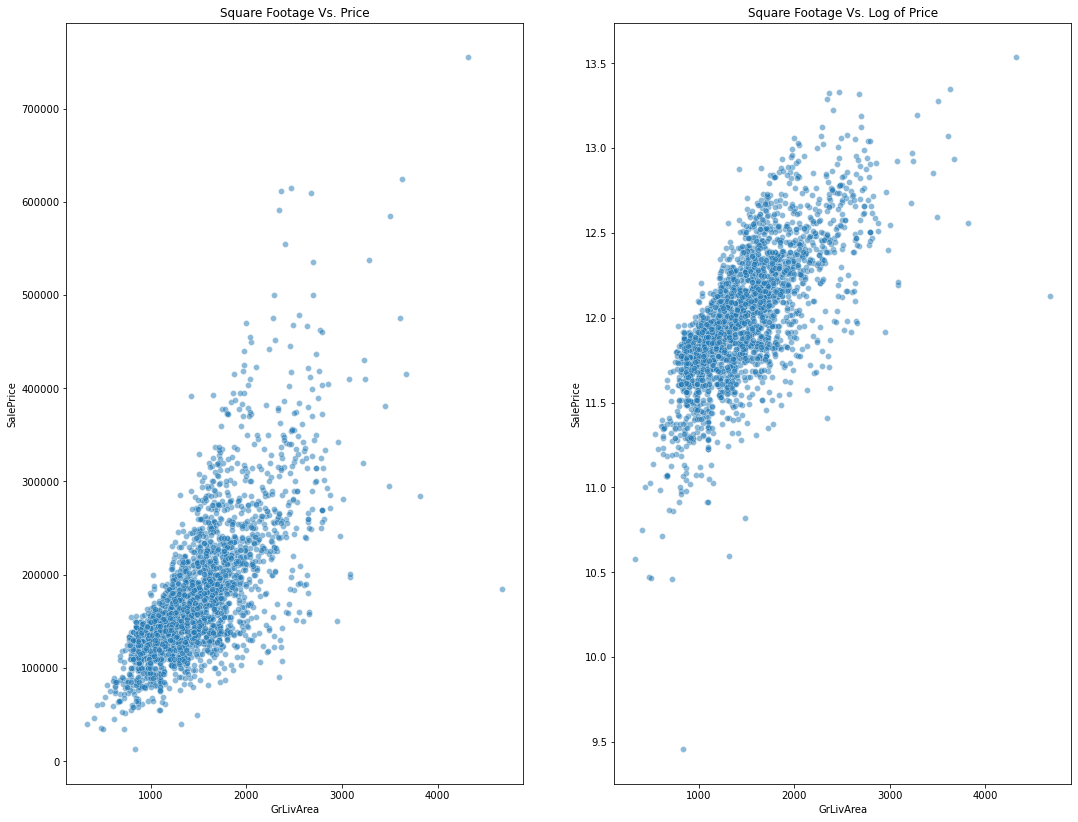
To make sure that linear regression assumptions are met, I apply log-transform to price for linear regression models.
It is common knowledge that a property's neighborhood can have a large impact on the price of the house. Please see the box plots by neighborhoods below.

Neighborhood was identified as important, especially by the linear regression model. I would have liked to explore this aspect in greater detail, but there is a large number of neighborhoods and a small number of observations for many of them. I believe that a larger data set would be needed to carefully address the neighborhood effects. On the positive side, many of the neighborhood characteristics can get absorbed in other variables, such as house quality, latitude, and longitude. XGBoost, the strongest single model I train, makes use of these features in price predictions. As a result, the Ames housing app shows the effect of location at a high granularity level.
Finally, I split the data into 20% validation and 80% training set in addition to the standard 5-fold cross validation split of the training set for hyperparameter tuning. I impute missing values using standard techniques of filling in with the median, imputing based on the group to which these values belong, deriving a dimension using a regression based on area, or filling in with zeros and None values where appropriate. To get the highest accuracy, I label-encode categorical features for the tree models or one-hot encode for linear regression models.
Model Selection
First, I run an experiment to identify promising models by producing model performance box plots for the initial key models to consider. I construct the box plots by measuring performance on the folds of 5-fold cross validation. In addition to the models below, I've also fit Catboost, which is not shown in the performance comparison since it is currently less integrated with scikit-learn.

The comparison above hints at the possibility of building an accurate linear regression model that could even outperform XGBoost. I test this conjecture by training both linear and tree-based models.
Part 1: Selecting and tuning for accuracy on the full feature set
For the highest accuracy model, I ensemble random forests, XGBoost, and Catboost. Random forests work best out-of-the-box (R-squared of .905) yet, as I confirm, that version is prone to overfitting given that the leaf node can be allowed to have one observation by default. Further hyperparameter tuning on random forest does not produce accuracy levels reached by the other two models, hence I assign only 5% importance to random forest predictions in the final ensemble. Catboost performs well with relatively little hyperparameter tuning (R-squared of .923) and trains relatively quickly given its ability to train in parallel, and I assign it 5% importance as well. XGBoost performs the best (R-squared of .931), albeit at the expense of training time. I ensemble the three model into a model having an R-squared of .932. To get an even more accurate model, I could train the model on more data or find additional strongly predictive features. Also, not all of the current features are highly predictive, and removing some of them improves generilizability while barely decreasing the model accuracy for XGBoost. I discuss this step in the subsection below.
Part 2: Further feature selection and reducing overfitting
With 83 features and only 2850 observations, I am concerned with the model overfitting to the noise in the features having low predictive power, thus lacking the ability to generalize. Indeed, the gap between train and validation set accuracies for the ensembled model above is about 6%, with the model having over .99 R-squared on the training data. To reduce the poor generalizability that comes with overfitting, I use Lasso and random forests as a feature selection step. More precisely, I use recursive feature elimination to select 30 features deemed most important by each of these models, take the union of both sets to arrive at 51 features, then use that set as an input to XGBoost.
The heatmap below shows the correlation of top 30 features selected by Lasso with log of sale price as a dependent variable.

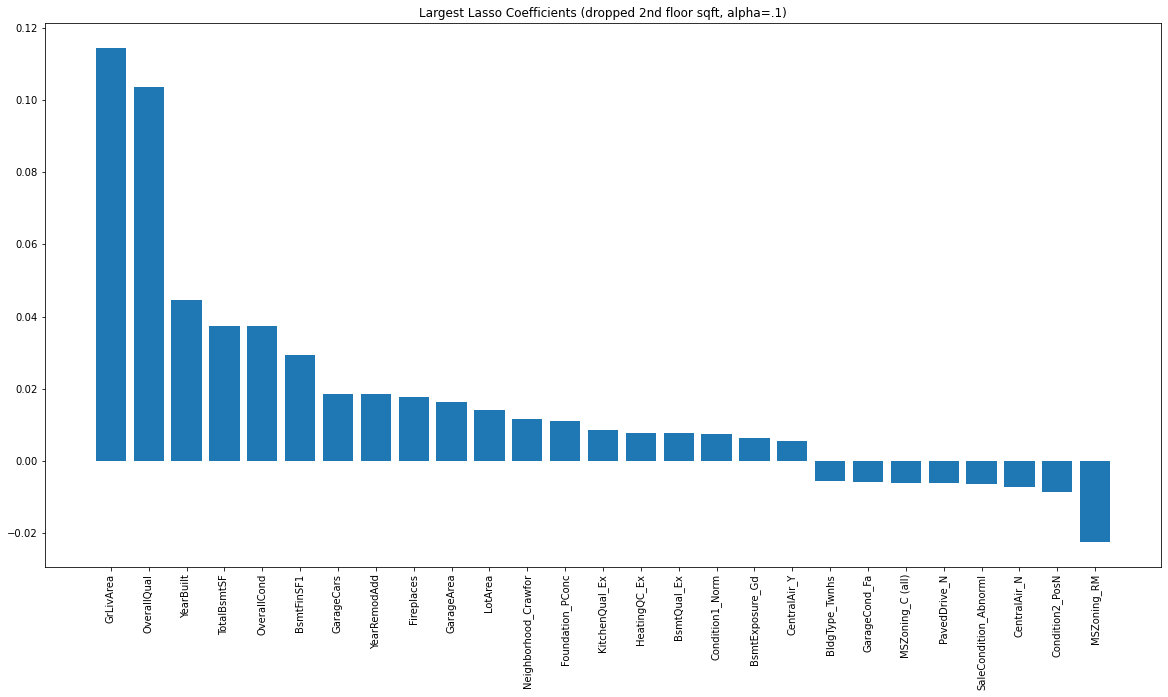
The plot below shows the largest Lasso coefficients
The feature importance plot below shows the most important features selected by random forests

Compared to training on the full data set, choosing the set of 51 columns leads to no loss in predictive accuracy while reducing overfitting. The highest accuracy XGBoost model has an R-squared of .933, slightly higher than the ensemble, while having about the same extent of overfitting. This suggest that I could retrain the models above on the reduced feature set without reducing accuracy. However, the improvements are likely to be in the thousandths and I believe that reducing overfitting is of greater importance than further tuning. The best XGBoost model in terms of offering a high accuracy while reducing the extent of overfitting has an R-squared of 0.93007 on the validation set and an R-squared of 0.97852 on the training set, thus having about 4.8% gap in train-validation set performance. This model strikes a good balance between accuracy and generalizability, and I argue for preferring this model to the ensembled model above: it is more likely to generalize to new data, and if the data changes in the future, it would be easier to re-train one model over an ensemble.
The feature importances from this model are shown below.

Note that overall quality is judged to be the most important by XGBoost, just as it is by Lasso and random forests. The living area, while also important, is ranked 6th by XGBoost and 2nd by both random forests and Lasso. As the second most important feature, XGBoost chooses the number of cars that could be parked in the garage. Lasso and random forests consider this variable to be slightly less important. All models also identify variables pertaining to basement as important: As briefly mentioned in the introduction, Ames is located along the Tornado Belt, making a basement and its quality highly desirable.
If one wishes to minimize the extent of overfitting, it is possible to tune XGBoost by reducing the number of estimators it can use. For example, by reducing the number of estimators to 380, I could obtain and R-squared of 0.91102 on validation set and 0.93838 on the training set, thus about 2.736% gap. However, a simple linear regression model is arguably a better alternative than XGBoost tuned with the purpose of minimizing overfitting. A linear regression model is highly interpretable, adds intuition about the data, and is easy to explain to stakeholders. I discuss it in the next section.
Part 3: A simple interpretable model
A linear regression model trained on the features selected by Lasso has moderate VIFs and highly interpretable coefficients with low standard errors. The dependent variable is the log of price, and to interpret the numeric coefficients, I take each coefficient's natural exponent, then interpret the result in terms of percentage change in price for a unit change in an independent variable. The coefficients and their standard errors are presented here for completeness.

Even a model with a small number of coefficients has an R-squared of above .90. Notice how the coefficients have sensible directions: having a higher (more recent) year built, greater overall quality/condition, or being in a nice neighborhood, for example, are associated with a higher price. Using the mean Ames house price of $178,060 as a reference yields the following estimates.

For example, an increase in a unit (square foot) of general living area is associated with $53 increase in sale price (notice, of course, that smaller houses are more expensive per square foot for other reasons). Each unit increase in year built is associated with $392 increase in price, newer houses being more desirable. Fireplaces are associated with an increase of $6303 in the average house price, not having central air conditioning is associated with a $12642 drop in price, each unit increase in overall condition is associated with $9348 increase in price, etc.
Deriving Business Value
For business purposes, I construct cap rate estimates. Cap rates are composed of the price prediction and net operating income (NOI) estimates. I will go over the parts of calculating NOI first. In brief, assuming $450/room estimates obtained by inflation-adjusting current Ames rental prices from Zillow, I obtain the following equation:
NetOperatingIncome=DistancePremium∙($450∙12 months∙NumberOfBedrooms∙(1-VacancyRate))-PredictedHousePrice∙CostsPerYear
I provide additional sources for the estimates used in the References section. The distance premium is 1.29 (29%) for homes half a mile or less from campus and 1.07 (7%) for homes between half a mile and a mile from campus. Similarly, the vacancy rates are 1.7% for homes half a mile or less from campus , 2.5% for homes between half a mile and a mile from campus, and 7% otherwise. Costs per year are composed of taxes, maintenance costs, insurance, and miscellaneous fees. I am able to find data on the first three for Ames, Iowa in particular, but the last one is harder to estimate precisely. The miscellaneous fees (legal fees, property management, etc) for general housing are know, and it is also known that these are higher for student housing. However, since it is hard to determine just how much higher it is, I use a conservative cost estimate of 3% per year.
Once the NOI is calculated, the cap rate is simply the ratio of NOI to the predicted house price. The return distribution for most homes in the test set is consistent with the 7 to 18% range. It would be helpful to consult a knowledgeable local real estate agent about the estimates above before using the app in production. I believe that the outliers are a result of my uncertainty about parts of the NOI equation, and can be removed by consulting with a real estate agent to get better estimates for those houses.

Once I obtain the price prediction and cap rate estimates, I store these in a data frame along with latitudes and longitudes. This choice reduces latency when deploying the application. I then build and deploy a Folium+Streamlit+Heroku app for real estate investors. Overall, the results align with what is knows about student housing choice decisions: Budget or middle-of-the-road houses outside of pricey neighborhoods make better choices for student housing.
Future Steps
There are some possible extensions of this work. As I already mentioned, consulting with a knowledgeable local real estate agent or agents is a must for more accurately pinning down the NOI estimates. In addition, my NOI calculations are based on the number of bedrooms in the house. It could be that a forward-looking agent can earn much higher returns on larger properties with relatively few rooms by partitioning the living area into suitable student living quarters. In a similar vein, including individual home’s regression coefficients can help an investor make forward-looking decisions with a view on improving the value of the home from the perspective of student housing.
The app itself can be improved by finding an additional database with homeowners’ phone numbers/email addresses and merging it with existing data, thus allowing an agent to go directly from using the app to contacting the homeowner. I did not make this choice to avoid introducing clutter, it may be beneficial to overlay the neighborhood lines directly onto the app for realtor’s convenience. Finally, the linear regression model can be further (slightly) improved by more advanced techniques (eg, hedonic regression), and if the stockholders require a highly interpretable model that is also more accurate, this would be a promising direction for future work.
Conclusion
For this project, I train a range of machine learning models, from highly accurate/less interpretable to less accurate/highly interpretable. I find that an ensembled model offers the highest accuracy, XGBoost offers a good balance of accuracy and interpretatbility, while a linear regression model offers highly interpretable results that can be shared with stakeholders. For example, fireplaces add $6303 to the average house price and central air conditioning adds $12642. I deploy these results in a Folium+Streamlit+Heroku app to help real estate investors earn high returns. Note that red indicates negative cap rates (losses) and increasing intensity of blue indicates higher profits.
For more of my work, please see the blogs on clustering and supervised learning in a marketing setting.
References
Data was originally available on Kaggle and the version used for this project can be found here
Calculating the cap rate using NOI
Renting houses in Ames, Iowa (approximately $450-500/room)

