Detecting anomalies in a statewide housing market with alternative data

This research was carried out under the supervision of haystacks.ai and was coordinated by the New York City Data Science Academy. A public version of some of the code used in the project is available on github.

Highlights

Our main task was to use alternative data to identify and characterize anomalies across a statewide single-family rental housing market. Some of the accomplishments of the project were primarily operational:

• Pipelines to bring in alternative data were developed, specifically data about schools, nearby entertainment and attractions, upscale indicators (e.g. Whole Foods, wine bars, ...), walkability and transit, crime, and natural risk to property.
• Alternative data has the benefit of being freely available, but can be noisy or course-grained in many cases. Useful signals from this data were extracted using feature selection and engineering, scaling, principal component analysis, and other methods

The anomaly analysis was to be carried out using a clustering framework. Some results of this analysis include:

• Traditional anomaly detection methods such as isolation forests and agglomerative clustering were tested first. Without further modifications, these methods detected statewide outliers, but failed to detect anomalies in many areas. They were also swayed by outliers with respect to the estimated average loss ratio and indicators of urbanity, as the majority of listings in Georgia are more suburban/rural.
• To address these issues, a localized agglomerative clustering technique was developed. The idea was to (i) break up the dataset geographically into overlapping regions, (ii) run the agglomerative clustering on data describing the listings in each patch, and then (iii) combine overlapping clusters transcend the arbitrary patches used.
• This technique allows clusters with larger intra-cluster variance than the global agglomerative clustering model, while still isolating the same number of listings. It was able to detect anomalies statewide and is less swayed by outliers.
• The localized agglomerative clustering technique allowed us to detect anomalies that are over $100K cheaper than houses in nearby clusters. The global anomaly detection methods focused on statewide outliers, concentrating on properties that are likely to be of little interest to investors in single-family rental properties.

Background

haystacks.ai is an AI/ML-driven company which helps real estate investors through predictive market intelligence and analysis. The primary objective of the research presented in this post was to answer a challenge given by haystacks.ai:

Can alternative data be used to identify and characterize anomalies across a statewide SFR housing market?

Alternative data presents an exciting opportunity for proptech, since it can incorporate factors missing from traditional analyses, and it is often freely (or, inexpensively) available. Examples of alternative data include public crime and risk data and information about points of interest, schools, and so on. In particular, this research was tested on scraped listings and information about the Georgia housing market.

However, alternative data also presents difficulties for anomaly detection. Alternative data can be noisy, and is often coarse-grained. Especially due to the coarse-grained nature of the data, traditional methods for finding anomalies may simply identify regions which have some property which is rare in comparison to the rest of the state, while ignoring many other 'true' anomalies.

Objectives

The project had two major objectives: (1) detect anomalies in the Georgia housing market, and (2) be able to evaluate anomalies in comparison to other homes, and see if they are overvalued and undervalued.

Ultimately, to complete the anomaly detection and analysis with reusable methods, a number of tools had to be developed:

• Scraping and ETL pipeline for alternative data sources
• Function library for creating geographically based features from alternative data
• Pipeline for building and analyzing PCA components quickly
• Traditional clustering pipelines for global anomaly detection (vs. all houses)
• Original clustering algorithm for local anomaly detection (vs. nearby)
• Toolkit for extracting anomalies and comparing them to nearby/similar houses

Anomaly detection goals

An additional stipulation of haystack.ai's challenge was that the anomaly detection should use clustering, and the solution should be developed alongside reusable, modular pipelines. Since the primary method of anomaly detection was to be through clustering, other desiderata were taken into consideration as well:

1. The model should be able to form clusters which are geographically contiguous
2. Anomalies should be in isolated or small clusters
3. Anomalies should be geographically spread out throughout a collection of listings

This research assumes models with these properties are desirable for a number of reasons.

Models meeting (1-3) identify anomalies which are over or undervalued for that region, which is relevant to investors seeking to develop in a certain area. It also suggests that true anomalies are not being missed at the expense of simply identifying areas with extreme values in comparison to the rest of the listings in the state. For example, in this dataset, listings in central urban areas attained certain globally extreme values, since most listings in Georgia are not in central urban areas. This research aimed to build models which were not restricted to only finding anomalies in certain areas with globally extreme values.

(1) independently is in accordance with a few assumptions about the clusters. One is that geographically contiguous clusters are relevant to the ultimate customer base. More important is their use in assessing the anomalies. If we are to compare an anomaly to a cluster of similar houses to see if it is overvalued or undervalued, the comparisons may not be valid if the clusters include houses spread across completely different areas.

Anomaly analysis goals

Though there were some global patterns in the anomalies detected, finding undervalued ones required manual inspection. This is somewhat expected, especially since there are often tradeoffs whose importance depends on the target renters/buyers (e.g. school quality vs. size or nearby attractions). Because of this, a toolkit for comparing an anomaly's price and other features to those of houses in similar or nearby clusters was also built.

Overview of the listings

The primary dataset consisted of real estate listings throughout Georgia scraped by haystacks.ai. Each entry contained information about a single listing, which could include price, square footage, room counts, year built, and/or a text description, along with latitude and longitude. Missing information about rooms or square footage was filled in with information parsed from a text description where available. Bathroom and half-bath counts were lumped into a single "bath" count.

Listings with extreme values were filtered out (e.g., extremely low prices or extremely high numbers of beds/baths), along with listings which were indicated as commercial or other non-residential properties. Listings indicated as 'lots' were dropped unless reasonable price, bed, and bath info was also available. This left a total of about 13,000 listings, which are plotted below.

Out of the original features, only price, square footage and bed and bath counts were ultimately kept. Lat/long was kept for plotting purposes, but was not used the same way (or at all) in the various models which were tested. Other data from the original dataset was not used except for the initial filtering.

Bringing in alternative data

Data were brought in from a variety of sources to provide more information about each listing. These primarily included data about:

• Schools
• Entertainment and attractions
• Upscale indicators (e.g. Whole Foods, wine bars, ...)
• Walkability and transit
• Natural risk to property
• Crime

A dataset of all schools in Georgia was scraped from greatschools.org, which included the location, Great Schools rating, and type of school (elementary vs. middle vs. high and public vs. private vs. charter). A dataset of walk, transit, and biking scores was also scraped for each zip code from walkscore.com. Information about natural hazards and associated damage from the FEMA National Risk Index (NRI) dataset was merged with the listings on census-level NRI tracts. Additional information about a large range of points of interest (POIs) were also brought in via the Google Maps API to create other features.

Since a large number of charter and private schools were missing ratings data, only public schools were considered. All public schools had ratings data. A total EAL Ratio feature was created from the NRI dataset. This was defined as the ratio of total estimated annual loss to buildings due to all risk factors divided by the total value of all buildings in the same area.

A function library was developed to create geographic features. Functions fell into two broad classes: (a) tools for merging the listings with region/map-based information (such as the NRI data), and (b) tools for computing information about POIs near each listing. The second toolkit can be further divided into functions which create different types of features: (a) ones aggregating information about POIs near each listing, and (b) ones which compute the distance between a listing and certain types of POIs. Haversine distance was used to compute distance in all cases, since both listing and POI location data was given in lat/long coordinates. The Haversine formula estimates the geodesic distance between locations given in lat/long.

Creating the features

A number of features based on aggregates were created for this model. For each listing, the average rating of the five closest schools which were within 30 km of the listing was computed. Also, the rating of the closest school was extracted. The total number of entertainment attractions within 20 km of each listing was computed, where an 'entertainment attraction' was defined as an art gallery, museum, or movie theater. The total number of overall attractions within 30 km was computed for each listing, which included a large number of types of POIs including amusement parks, bowling alleys, art galleries, bars, cafes, clubs, restaurants, and other non-retail destinations. Other totals included the Whole Foods, Starbucks, wine bars, and breweries within 5 mi of each listing, together referred to as the 'posh' POIs.

The distance to the nearest POI of a certain type was also computed for various types of POIs. These included parks, malls, an entertainment attraction, transit station, and 'good' elementary school, defined as elementary schools with a Great Schools rating of at least 7/10.

Total property crime rates and property theft crime rates were also merged with the listings at the zip code level. From the NRI data, the estimated annual loss to buildings due to various prevalent natural risks was also selected (tornadoes, strong wind, lightning, heat and cold waves, and hail).

Feature selection and transformations

Some features were transformed with logarithmic or power transformations to make them approximately normal, if possible. Of the 32 features derived from the listing information and alternative data, 17 were selected before applying PCA. Some highly correlated features were removed (e.g., Bike Score was removed since it was highly correlated with Walk Score). In other cases, a feature with non-normal distribution was removed if there was another feature with more normal distribution which captured qualitatively similar information. Other features were removed if they contributed little to the overall variance of the data. For example, all NRI data except the EAL Ratio were removed for this reason.

It is worth remarking that EAL Ratio has a large right tail, with many listings over two standard deviations above the mean. Though some other NRI features which were not used have more normal distribution, EAL Ratio was kept for reasons described in the this section. A map showing the distribution of this feature is shown below, which shows that many of the outliers in the right tail are concentrated in a few areas.

Principal Component Analysis (PCA)

While clustering generally suffers when using many features, dimensionality reduction can be applied to large feature sets to get simpler representations. Clustering algorithms also generally require that data be properly scaled. This research used a scaling and PCA pipeline to describe each house using five features. Each of these five features is called a principal component (PC). Since only five PCs were used, clustering can be applied more effectively. Additionally, this allows the data to be more easily visualizable, and can reduce some noisy variance.

Importantly, the features which were put in the pipeline did not include any location-specific information (like latitude and longitude), but only information about the house size and price, together with the features constructed from the alternative data. These features did not include reference to specific locations, only metrics derived from nearby attractions of various types. Lat/long were left out, as processes involved in scaling and dimensionality reduction breaks their geographic interpretation. Most out-of-the-box methods of normalizing and reducing the dimensionality of features do not make sense when lat/long are mixed with other data types.

Summary of the principal components

Five PCs were used in this research.

• PCs 1 and 2 correspond to urban and upscale suburban features, respectively
• PCs 3 and 4 are corrective components, respectively representing a tradeoff between a larger home vs. higher crime/worse schools, and better schools/suburban attractions/walkability vs. higher crime/decrease in posh POIs
• Areas with listings with high PC1 (over 2.5) are in urban areas, though the majority of listings in Georgia have PC1<2.5
• Many houses with large PC2 are distributed along the line where PC2=PC3, which corresponds only to increased price and house size
• There are more outliers on the higher end of this line (larger, more expensive houses), than on the negative side
• Though there are a number of larger, more expensive outliers, they are split by the PC2=PC3 line into homes with lower crime and access to better schools, and those with higher crime and less access to good schools.
• PC5 almost entirely identifies areas with high EAL Ratio. High PC5 is localized to an area around Savannah, the southwest, and a small area northwest of Atlanta.

Only the first five components were chosen, since these account for 78.3% of the variation in the full dataset while allowing the clustering algorithms to behave as expected. The loadings of these first five PCs are shown below. Features whose weight is near zero in a particular PC contribute little to it, while values near 1 or -1 indicate that full value of the feature is added or subtracted to create that PC.

A more thorough analysis of the distribution of the data in PC space and geographic distribution of the PC values is provided in section beginning with Overview of PCs.

PCA Pipeline

To implement PCA, a pipeline was built which:

1. z-scores the data
2. uses PCA to choose new axes for the feature space, then
3. provides 'loadings'

(1) guarantees that the center of the feature space (all values = 0) corresponds to having the average value for each feature, and moving 1 unit along any axis corresponds to an increase in that feature by one standard deviation. After (2), the most variance lies along the first axis, the next along the second, and so on., and there is no covariance between distinct axes (PCs). These axes can be described as a weighted sum of the original feature vectors. Step (3) provides a visualization and numeric representation of these weighted sums or 'loadings'.

Overview of clustering methods

Recall that there are three goals for the clustering and anomaly detection method. Agglomerative clustering (AC), DBSCAN, and isolation forests were all considered as they do not require the number of clusters to be set in advance, which made them more amenable to being combined with certain pipelines, and it is easy to tune them to produce a certain number of anomalies. All models can be tuned to satisfy (2), but all struggle with (1) out of the box when lat/long information is not used. We took (3) into consideration when evaluating the models.

For all models, listings which had imputed values were not considered as candidates for anomalies. Out of the 13,086 listings in the dataset, this left 10,774 listings which could be classified as anomalies. Each model was tuned to produce approximately 150 anomalies, accounting for about 1.4% of the total listings considered. We then compared the geographic distribution of the anomalies detected by each model, along with the distribution and sizes of non-anomaly clusters where relevant. Tunings detecting 3% and 5% anomalies were also considered, but had similar results.

AC is based on the premise that observations that are closer together according to a specified metric should be grouped together first.  AC does not satisfy (1) & (3) out-of-the-box, and it is not clear that location can be incorporated into the data in a reasonable way for AC. However, we introduce a localized version of agglomerative clustering which does satisfy each of our criteria.  We discuss AC in more detail in this section, and the results of global and local AC here and here.

Isolation forests have been used for anomaly detection to identify instances of money laundering, for example. The key idea of the algorithm is to recursively generate partitions of the sample by selecting a random attribute and selecting a random split of that attribute within that attribute’s range. This contrasts with random forests, which choose the best split in terms of reducing the impurity, for example. The premise of using isolation forests for anomaly detection is that anomalies take fewer splits to isolate from the rest of the data. The listings which can be isolated with the fewest splits are identified as anomalies, up to the number of listings specified by a threshold, such as 1.4% of the data.

DBSCAN is hypothetically capable of satisfying (1)-(3) if lat/long were used as well, but it is not adapted for dealing with lat/long data in conjunction with non-geographic features out of the box either. DBSCAN’s key idea is grouping together observations in high density regions and identifying remaining points as anomalies.  It is possible that it can be adapted to work with mixed location and other data with more nuanced scaling and a carefully chosen metric.  We will discuss potential fixes to DBSCAN in more detail in Future steps, but did not test it in this research.  

Isolation Forests

While isolation forests are fast (linear time complexity), have low memory requirements, and are insensitive to scale, they only solve part of our problem. However, their success in anomaly detection made them a good benchmark. Isolation forests only create two clusters: anomalies and non-anomalies. While this can help find anomalies, it does not create meaningful clusters of non-anomalies to compare the anomalies to. The lack of meaningful comparison points is particularly challenging since without houses that serve as a benchmark for a potential anomaly, it is nearly impossible to determine that anomaly’s value to potential investors.   

Additionally, the anomalies detected are almost exclusively in high PC5 and urban areas. It is likely that these areas are split off first, since they are the most dissimilar from the rest of the dataset. This could be interpreted as the algorithm showing geographic bias on this dataset. While the identified listings may be outliers among all the listings in the state, this method misses potential anomalies in other areas. Since this method detects these anomalies at the expense of finding them in other areas, we believe that this method of anomaly detection would not be the most useful for investors.

A map of the anomalies detected by this model is shown below, together with comparisons to high EAL Ratio and urban areas. The urban areas identified as Cluster 1 were found by an initial k-means clustering run to facilitate EDA, as described in this section.

Since isolation forests are not sensitive to scale, we can adjoin lat/long information directly to the PC dataset. However, this does not change the geographic bias phenomenon, and in fact anomalies are more restricted to the high EAL Ratio area.

AC global clustering

AC models work by iteratively combining listings into larger and larger groups. The particular variant we used decides whether to merge clusters based on the overall increase to within-cluster variance. More details on AC and why this variant was used can be found in this section. Unlike isolation forests, AC can be used both to identify anomalies, and group houses into clusters based on similarity. Another major difference is that AC necessarily looks at all the features at once when determining if clusters should be joined.

A baseline AC model was run first on the five PCs alone. Though the PCs do not contain location data, which may prevent the model from being able to fulfill the first desideratum of forming geographically contiguous clusters, this model was run to evaluate: (1) to what extent do clusters in the PCs already correspond to geographically contiguous clusters, and (2) to what extent do these PCs cause a 'geographic bias' issue for AC on their own? We refer to this model as the global AC model.

Results

This model used AC applied globally to the entire set of listings according to their PCs alone.

• Tuning to approximately 150 isolates required the model to split hairs, breaking the clusters down to 'dust', with all but the largest group containing fewer than 30 houses
• The PCs alone did not create geographically contiguous clusters, with many clusters containing listings spread throughout the state
• Anomalies which were detected tended to be in areas with high PC5 or urban areas, indicating that these properties are what the detection method was attending to
• However, this model may be useful for detecting "global anomalies", or identifying larger clusters of similar houses which are outliers when compared to the rest of the data.

We interpret the large number of very small clusters as indicating a difficulty in identifying anomalies while simultaneously forming generalizations about the remaining houses. We interpret the last bullet as showing 'bias' of the model towards identifying the global outliers along these dimensions as anomalies on this dataset. The effect is reduced, but still visible, at different tunings.

Discussion

The model was first tuned to isolate 154 listings, which is about 1.4% of the total listings which could be identified as anomalies. Over 2500 clusters were needed to isolate this many listings. Of the top 10 largest clusters, all but one contained fewer than 30 listings. The clusters quickly drop to containing 20 or fewer listings each.

The large number of clusters, which are mostly very small, might be interpreted as a failure to capture generalizations about the homes. That is, when applied globally, AC has to split hairs to isolate approximately 150 listings. As might be expected, many of these clusters were geographically spread out, as no location information was available to the clustering algorithm. The six largest clusters are shown below.

Though the clusters themselves may be geographically spread out, the anomalies are more concentrated around a few areas, though less severely than with isolation forests. Plots showing the geographic distribution of the anomalies detected by the global AC model, as well as how it compares to the distribution of the urban and high PC5 areas, are shown below.

Though much less than the isolation forests, the global AC model appears to still have some 'geographic bias' in its anomaly detection. Like with isolation forests, anomalies were more concentrated around areas with high PC5, which is mostly made up of EAL Ratio. Unlike with isolation forests, global AC detected anomalies in the urban areas as well when tuned to the same number of isolates. However, some large areas with many listings - the entire region in the southern central and eastern part of the state, the outer suburbs of Atlanta, and an area to the northeast of Atlanta - have few to no anomalies.

As more anomalies are admitted, the geographic distribution tracks that of the whole dataset more closely, whether through dropping the threshold (making smaller clusters, which omit more listings), or looking at clusters larger than isolates (such as pairs or triples). However, both types of adjustments still display some geographic bias, in that the distribution of anomalies tends to expand from the areas with concentrated anomalies as more are admitted. Other tunings are shown in the model comparison.

Local AC model

As mentioned in the explanation of the principal component analysis, there is no obvious out-of-the-box way to mix lat/long with the other numeric features which were used to create the PCs in a way which respects their geographic interpretation. We introduce an original modification to AC in order to incorporate lat/long in a way which keeps the clusters and clustering process interpretable, which we refer to as local AC.

Motivation

The idea is to introduce lat/long in a heterogenous way, which treats it differently from the remaining features. The algorithm is based on two key ideas:

• Do not include location in the data to be clustered (don’t use it to measure similarity)
• Instead, use lat/long to only allow the detector to see a small portion of the map at a time

These ideas were motivated by a few assumptions about the algorithm:

• Since it only looks at a small region of houses at a time, the model should be thrown off less by features which are heavily skewed towards particular geographic areas, since most listings in the region will show the same skew.
• Since it will only look at merging clusters containing nearby houses, the clusters should be more geographically contiguous.
• Since it will only ever compare a house to those nearby, it should be better at detecting 'local' anomalies - houses which are significantly different from houses around them, even though they may be similar to houses in other, faraway areas.

The main difficulty in applying such an algorithm is that clusters of similar houses may span the particular geographic windows chosen. For this reason, AC was applied through an off-label usage of the Kepler Mapper, based on the more general concepts of Reeb graphs and the mapper algorithm, together with an analysis of the graph output by the mapper.

Altogether, our implementation of the mapper algorithm can be summarized as follows:

1. Break the dataset up into listings in overlapping 'rectangular' geographic regions by lat/long
2. On each region, run agglomerative clustering on the PCs alone.
3. Combine any clusters containing a house in common until the clusters are all disjoint.

The first step is done so that we can detect clusters which span multiple chunks of the map. The second step is where the clustering algorithm applies. These clusters are based only on the PCs, and not lat/long, like with the other models. The third step is used to 'glue' clusters together which span multiple map regions. An illustration is provided below.

Wrapping AC in this method provides new tunable parameters, which allow the geographic span and spread of clusters to be controlled separately from the threshold, which is a cutoff only in terms of similarity. The number of chunks the map was broken into was left fixed, so that listings would not be put in clusters where all other houses in the cluster were over roughly 10-15 miles away. However, the percent of overlap between the map chunks can be tuned to change how much clusters can spread geographically.

Results

• Tuning to 150 isolate still required many clusters, but about half as many as global AC
• The 10 largest clusters were significantly larger than those in global AC
• Anomalies were spread geographically throughout the state
• Even large clusters are geographically contiguous, but can have varying geographic span

Discussion

Though local AC saw the same data as global AC, it only looked a small region of the map at a time. After that, overlapping clusters are glued together. As a consequence, the threshold could be raised much higher, allowing clusters with larger variance than the extremely strict global AC model, while still isolating the same number of listings. AC threshold (modulating how similar houses in a cluster are) and the overlap between chunks of the map (modulating the geographic spread of clusters) were tuned in tandem to produce approximately 150 isolated listings, while also maintaining a reasonable spread of cluster sizes among the largest clusters.

In comparison to the global models' 2500 clusters, the local AC model was tuned to create 1248 clusters to isolate 156 listings. While all clusters formed by global AC contained 32 or fewer houses, the largest clusters formed by the local AC model were much larger, with all of them containing 97 or more listings. The model was tuned to produce these results, as these cluster sizes seemed reasonable considering that all listings in a cluster should be both similar and in a geographically localized area. The sizes of the 10 largest clusters are plotted below.

Maps of the largest clusters show that clusters also stay geographically contiguous.

In contrast to both the global AC and isolation forest models, the anomalies detected by the local AC model were geographically spread out throughout the listings.

While local AC still detects anomalies in the high EAL Ratio and urban areas, the anomalies are much more geographically distributed throughout the state. In particular, the south central and eastern region, the region to the northeast of Atlanta, and the outer Atlanta suburbs which were devoid of anomalies in the global AC model have more anomalies identified in them in the locally applied version.

Additionally, we can be more confident that the anomalies which were identified are dissimilar from nearby houses. A listing only remains isolated if it cannot be put in a cluster with any house within about 10-15 miles, even though the AC threshold is much higher than in the global case (threshold = 2.6 vs. 1.28).

Comparing the models

For both AC models, isolated listings were considered anomalies. With an isolation forest, listings are identified as anomalies if they can be quickly isolated by the random forest. All models were tuned so that approximately 150 listings were classified as anomalies. This accounts for about 1.4% of all the listings which are being considered for classification (about 1.1% of the entire dataset). While AC also creates clusters of non-anomalies, the isolation forest only distinguishes between anomalies and non-anomalies. Hence, only with AC models do we get groups of similar houses which can be used as a point of comparison against the anomalies.

When an isolation forest or global AC is run on the PCs, the anomalies are concentrated in a few areas. For both models, areas with high PC5, associated with high EAL Ratio, show a concentration of anomalies. Global AC also has anomalies in urban areas, as does the isolation forest, though neither identify many anomalies in other areas. As the models are tuned to identify more listings as anomalies, the geographic spread of anomalies increases. However, it can still be seen that the added anomalies mostly emanate from the existing concentrated areas.

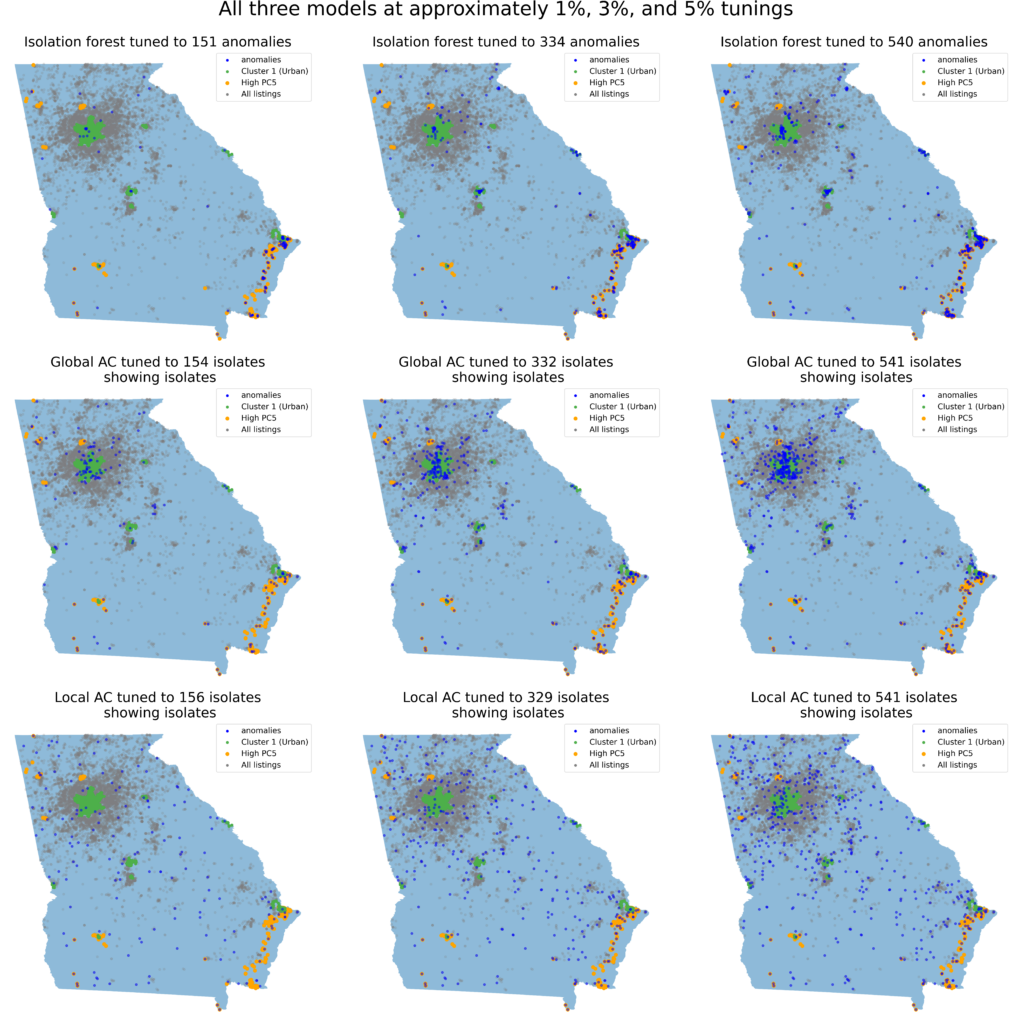
Moving from left to right shows the results as each model is tuned to identify a larger and larger percentage of the data as anomalies. For isolation forests, this is done by raising the 'contamination' level, and for AC this was done by lowering the threshold which allows two clusters to merge. In the AC case, this has the effect that there are more overall clusters, since fewer can be combined. This means that listings are less likely to be grouped with others, thereby increasing the number of anomalies.

Isolation forests and global AC all show heightened concentration of anomalies in the high PC5 (high EAL Ratio) and Cluster 1 (Urban) areas across tunings, while detecting few anomalies elsewhere. With local AC, anomalies are added more evenly around the map across tunings.

With AC, we can also change the cutoff for the size of the clusters we consider anomalies. So far, only isolates have been considered anomalies, but clusters containing only 1, 2, or 3 houses might also be considered anomalies. However, as this cutoff is raised, the distinction between the local and global AC models becomes even more apparent. Raising the cutoff on the global model is very coarse, since clusters already have to be very small to create the isolates; moreover, the bias towards urban and high EAL Ratio remains strongly visible.

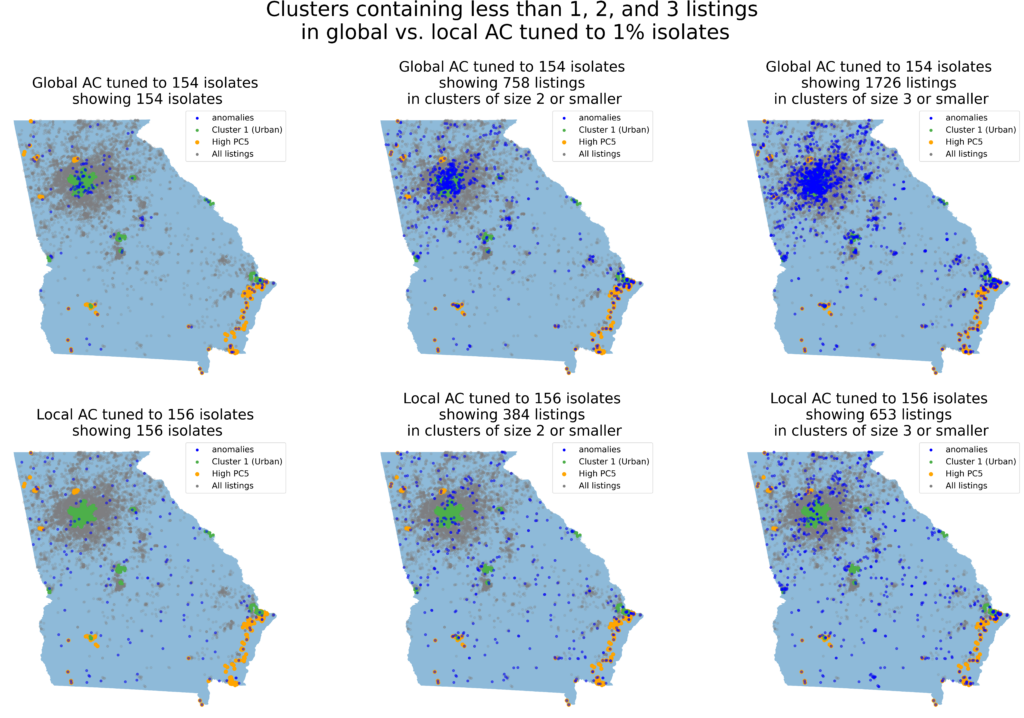
The above examples show that global AC continues to show the geographic bias in the distribution of the identified anomalies, whether the threshold for AC to form clusters or the cutoff for cluster size is changed.

We could directly add lat/long data to the PCs with isolation forests, as they are insensitive to scale. However, that cannot help form geographically contiguous clusters (since isolation forests do not form clusters with the non-anomalies), and in this case it did not improve the geographic bias. We introduced one method of adding location data to AC (local clustering), but others could be considered. This deserves further attention, and some discussion is given in the Future steps section.

Analysis of specific anomalies

Once anomalies were identified, they were analyzed to identify whether or not they would make good investments. As remarked in the anomaly analysis goals, it is often difficult to say whether an anomaly is objectively good or bad, as it may differ from other houses along many dimensions, some of which may be tradeoffs between different desirable features. For this reason, an anomaly analysis toolkit was developed. This included tools for:

• Plotting anomalies on a map, and in the space of PCs
• Finding the clusters containing the houses most similar to a given anomaly (in terms of having the most similar PCs)
• Finding the clusters containing the houses closest to a given anomaly (in terms of geographic distance)
• Comparing an anomaly to other listings and clusters of listings

In order to draw comparisons, we can look either at the PCs which were used to cluster the data, or the original data associated with the listings. While raw prices were extracted from the listings (prior to imputing values, scaling, or dimensionality reduction), anomalies were otherwise compared to other houses and clusters in terms of the PC loadings, not the original features. This made it possible to get interpretable comparisons in terms of the original features, but using the collapsed, dimensionality-reduced version of the features. This way, it was more apparent why particular anomalies were left out of nearby or similar clusters, since the comparisons only used data the models had access to. The toolkit provides these comparisons between loadings, as well as price comparisons, in addition to finding the similar and nearby clusters.

Aggregate results

For each method, a histogram comparing the differences of anomaly prices to the prices of houses in the most similar clusters was built.  This allowed us to see how many anomalous houses are above or below the prices of those in similar clusters.

For the global version, the differences in price between each anomaly and the average price of the houses most similar to it were roughly normally distributed, with a long right tail.  Anomalies in the left tail (lower 2.5%) were examined closely. In the local version, the aggregate difference is $40M for anomalies cheaper than the houses most similar to it, and $46M for those which were more expensive.  Once again, anomalies in the left tail (lower 2.5%) were examined closely. The distributions of price differences are shown below.

Individual anomalies

We know from the section on global AC that the anomalies detected by this model are concentrated in urban and high EAL Ratio areas, indicating that many anomalies in other areas are likely being ignored. Additionally, since tuning this model required many small clusters, and clusters could be widely geographically spread out, finding legitimate comparisons was difficult. For many of the anomalies detected by global AC, the listings in the clusters containing the listings most similar to the anomaly were often in completely different geographic areas. An example is provided below.

In the anomalies detected by the local clustering method, a few key patterns emerge: (i) Many of the anomalies have fewer beds but higher square footage,  (ii) most local anomalies are not found by the global model, and (iii) most anomalies belong to small localized clusters. Points (ii) and (iii) are clear benefits and are exactly the desiderata that are not provided by the global model.  Further research revealed that homes with an open floor plan appreciate faster than most other types of homes, implying that (i) is also a strong benefit.

The six houses from this model which were examined closely have prices that are generally $100K-$500K lower than surrounding houses.  Some of these houses border million-dollar properties in highly desirable neighborhoods.  These houses are generally lower in one or two dimensions in the feature space, yet higher in one or two other dimensions.  Below, we examine a few of these anomalies closely, referring to them by their index numbers in our data set.

• House 7639, located in the North Central part of Georgia, is $500K cheaper on average than houses in nearby clusters, slightly smaller and farther away from transit, yet is at least as good in other dimensions.
• House 7720 is $130K cheaper than houses in nearby clusters, has a slightly higher crime score, much better walk score, and a high number of attractions nearby.  It is also very close to an upscale neighborhood.
• House 12653 is $187K-$600K cheaper than houses in nearby clusters, has slightly worse schools, lower transit access, but larger square footage than the surrounding areas. It also has fewer beds and baths than the surrounding houses (probably an open floor plan). It also has lower estimated average loss and  a comparable number of nearby attractions to houses in nearby clusters.

Details

The sections below contain a more detailed analysis of the PCs and models used. These provide justifications for some of the choices made and interpretations given, as well as more thorough analysis of the distribution of the listings as a whole.

Overview of PCs

Large positive values of PC1 - the first principal component - indicate high values associated with urbane features - closer than average distance to transit, and higher than average walk and transit scores, nearby attractions, but also property crime rates. Large negative values of PC1 indicate the opposite (lower than average walk scores, number of attractions, etc.). On the other hand, all features involving schools, price, and house size have small (slightly negative) weights, indicating that they contribute little to PC1. Large positive PC1 would only correspond to slightly lower than average school quality and house size, but significantly elevated transit scores, attractions, etc.

By contrast, PC2 is an indicator of upscale suburban features (larger house, better schools, lower crime), while the other features do not contribute as significantly to it. PC3 and PC4 act as 'correction' components. PC3 represents a tradeoff between larger houses and higher crime with worse schools (with walk scores and attractions relatively fixed), while PC4 represents a tradeoff between better schools and fewer attractions with worse crime (with house size relatively fixed). PC5 is dominated by the high-variance EAL Ratio feature.

Despite the fact that PC5 mainly highlights certain geographic areas associated with high EAL values, it was kept in the analysis for two reasons. (1) Even with the large variance, there was little reason to suspect the outliers were incorrect, and (2) retaining this feature helped examine how different models handle the uneven variance which can naturally appear in settings using alternative data.

Interpreting the PCA features

To get a sense of how the top five PCs characterize the listings, and what geographic areas they indicate, the data were clustered using k-means (with no additional geographic information, such as latitude/longitude). Three clusters were chosen by a standard elbow plot test on the inertia and because increased components did not provide additional clarity to the distribution of the data in the PC space. These clusters are plotted geographically below:

Areas with houses in Cluster 1 all correspond to urban areas (namely, Atlanta, Savannah, Augusta, Macon, Columbus, and Albany). We will see that areas with homes in Cluster 2 correspond to those with high PC2, i.e. upscale suburban areas with larger houses, access to better schools, and lower crime. Areas dominated by Cluster 0 homes represent the more typical case of suburban and rural areas.

While it is no surprise that the listings are broken into urban/upscale suburban/general suburban and rural groups, it is important to note that these groups track the PCs alone, and do not arise from location-specific data (such as latitude and longitude). The properties of the houses together with the features derived from the alternative data are sufficient to distinguish these different areas, without taking the particular locations of the listings into account.

The plot below shows all of the listings plotted according to their first 3 PCs, and colored according to the major clusters. An interactive plot is also provided here.

As expected, listings are concentrated near the origin, with many points distributed in a spherical region around it. This main sphere is split in half at PC2 = 0, with listings with positive PC2 (more upscale) falling into Cluster 2, and listings with negative PC2 falling into Cluster 0. Listings in the urban Cluster 1 are largely those with PC1>2.5. While most of the listings are within a distance of 4 from the origin, there are outliers beyond this radius. The plot of PC1 vs. PC2 shows that there are different types of outliers outside of this sphere, some with a pronounced increase in PC1, the others in PC2.

Correction components

While this plot is revealing, it is important to remember that PC3 and PC4 are 'correction' components, and how the data are distributed along the first two PCs in combination with these corrections must be checked. Viewing the data from the side shows why this is necessary.

The data appear to be distributed along the line where PC2=PC3, especially among the outliers with large PC2. A dotted black line is used to indicate this line in the plot. Moving along this line in the positive direction corresponds to larger PC2+PC3. Since most listings with large PC2 also have larger PC3, we provide the loading associated with PC2+PC3.

Most of the features do not contribute to this loading except for price and house size. Hence, moving further in the positive direction along the PC2=PC3 line simply corresponds to increased house price and size, while moving in the negative direction corresponds to decreased price and size. Importantly, PC3 cancels out much of the contribution from features associated with schools and crime in PC2, so that listings along the PC2=PC3 line are closer to average in these respects. Areas with high PC2+PC3 correspond with houses significantly larger and more expensive than the average, and mostly occupy an area to the immediate north of Atlanta, shown below.

Moving away from the PC2=PC3 line corresponds with moving parallel to the blue dotted line above which is perpendicular to it. Moving down this line is associated with increasing PC2-PC3, whose loading is provided below.

Hence, the listings lying below the PC2=PC3 line correspond to listings with increased nearby school ratings, closer high-quality elementary schools, and lower crime. This shows that while outliers lying far out along the PC2=PC3 line are larger, more expensive houses, only those also lying significantly below it have the added benefits associated with the upscale suburban houses. The geographic distribution of PC2-PC3 is provided below.

Areas with high PC2-PC3 are associated with better schools and lower crime. This makes all of the north area of greater Atlanta desirable to those where schools and crime rates are a priority. The area of north Atlanta described above would hence be especially desirable, as it reaps all of these benefits while also having larger homes.

We finally confirm that the listings within the circle are in fact roughly normally distributed, while the outliers are distributed along the PC2=PC3 line. Distribution plots of PC2 and PC3 are provided below in the form of a contour plot and 3d histogram.

These plots confirm that the data are roughly normally distributed in PC2 and PC3 near the origin. Outliers are in fact mostly distributed in the positive direction along the PC2=PC3 line, indicating more outliers which are larger and more expensive than the average than smaller and cheaper. Somewhat surprising are many large and expensive houses lying above the PC2=PC3 line, associated with higher crime and worse schools, making large homes in areas with good schools and lower crime more of a rarity.

The corrective PC4 is loosely normally distributed over PC2 and PC3, shown in the plot below and interactive plot here.

On the other hand, it is important to view PC4 in combination with PC1, especially since its components corresponding with 'posh' points of interest cancel out those of PC1. The plot of PC1 vs. PC4 is shown below.

Higher values of PC4 are associated with fewer 'posh' points of interest (thought other points of interest like movie theaters, gyms, etc. may still be in the area). Though extremely high values of PC1 are associated with elevated PC4, the urban Cluster 1 lies below the PC1=PC4 line, so that the contribution of PC4 is not so great as to cancel out the urban features indicated by high PC1. However, the plot does show that looking at PC1 alone gives an inflated sense of the urbanity of an area, since PC4 does counteract some of the urban features of PC1.

PC5, dominated by EAL Ratio, is loosely normally distributed throughout Georgia, but has significant right skew, which is comparatively exaggerated after z-scoring. As a consequence, PC5 largely serves as an indicator for those regions with high EAL Ratio, namely some houses near Savannah in the southeast, homes in the southwest of the state, and a small group of homes to the northwest of Atlanta.

What is agglomerative clustering?

The main clustering technique examined in this research was agglomerative clustering (AC). AC does not require that the number of clusters clusters be specified in advance. Rather, AC starts with every listing in its own cluster, then begins to merge clusters iteratively. Unlike isolation forests, AC looks at all features at the same time, and hence might avoid the issue that they ran into. Additionally, the AC method was amenable to being used with the Kepler Mapper to implement the local clustering approach.

Here, a Ward linkage criterion was used. It gives the most regular sizes, and is less susceptible to a 'rich getting richer' effect than other linkage criteria, where large groups tend to dominate quickly. The linkage criterion is way that the metric is used to determine if two clusters will be merged at a certain step. The Ward criterion is based on the increase in the total within-cluster sum of the squared errors. Specifically, the Ward distance between two clusters is shown below, and is similar to an ANOVA test trying to determine if the clusters are drawn from groups with different means.

The top version makes the analogy to an ANOVA apparent, and can be viewed as comparing two sums of squared distances from each point to a mean: the first over the cluster which would be formed by merging A and B, and the second over the two clusters prior to the merge. The difference represents the overall increase in the total sum of squared distances from the cluster means (centroids) if the two clusters were to be merged. The bottom version gives a different perspective: the Ward distance between two clusters is the squared distance between their centroids times half the harmonic mean of their respective sizes. In this way, merging two clusters is penalized partially based on the distance between the (centroids of) the clusters, and partially on their sizes.

Since Ward distance makes use of the sum of squared distances, the norm indicated by | · | must be the Euclidean metric. This is the main limitation of the Ward linkage criterion. However, this metric and criterion make sense for our data, since the features are (a projection of) z-scored, numeric variables. Other common metrics, like L1 (Manhattan distance), do not make as much sense on PCs, since the PCs are already (projections of) rotations of the original features, so coordinatewise comparison of values is already making comparisons across multiple features of the original feature space.

The only remaining tunable parameter for the basic model is then the 'distance threshold': the value which sets a limit on the Ward distance between two clusters which can be merged. When all remaining clusters are separated by a Ward distance at least as great as this threshold, the algorithm terminates. This parameter can be tuned to produce a desired number of anomalies, and hence AC models can be tuned in such a way that makes it possible to compare their anomaly-detection results to other models.

Alternative approach and future steps

Adding lat/long approach

Instead of using local clustering, we may consider adding lat/long into the dataset being clustered in order to create geographically contiguous clusters. While adding lat/long to isolation forests is more straightforward, as they are insensitive to scale, adding it to AC models is more nuanced.

• It does not make sense to feed lat/long into a scaling and dimensionality reduction pipeline with the other features, as it will destroy the geographic meaning of the features, as mentioned in this section, so location data cannot be incorporated this way.
• The variety of AC considered here (Ward clustering) puts features in direct competition.
• Were location information to be included with the other features, there would be a direct tradeoff between geographic span and variance among other features
• That is, when comparing two clusters with the same variance, the cluster with smaller geographic span would have more variance among the remaining features.
• This kind of model did not seem to accurately describe the business case here.

Despite this, we ran a global AC model on the dataset of the five PCs together with lat/long as a baseline. This showed some improvement over the global model without LL but similarly required 2,424 very sparse clusters to isolate approximately 150 listings. As with the global model without LL, this makes it hard to compare houses to other clusters, as they will be very small and may miss generalizations.

It is difficult to interpret this model, partially due to the reasons listed above, but also because the metric used does not make much sense when mixing lat/long and other features. While the other features are projections of z-scored features, lat/long have a much larger range, and so their contribution to the overall variance is distorted. Still, it was clearly not the case that this model simply relied on lat/long: global AC applied only to lat/long actually identified areas other than urban areas as anomalies, since in this case, 'anomaly' just means 'geographically isolated.'

A more fair comparison would then involve choosing a better metric. One metric considered was a 'haverdot', consisting of the squared distance between two listings plus the dot product of their PCs. This metric behaves the same as the typical Euclidean metric used on the PCs would, as if the locations of the listings were given in such a way that their dot product actually came to their squared distance. However, implementing such a metric would have involved modifying the sklearn algorithms used elsewhere, as they currently do not support custom metrics with Ward AC.

Such an implementation might improve traditional global AC. If a weight were additionally put in front of the terms representing the distance between listings, we could also control the effect of location on the clusters independently of the other features, as with local AC. In any event, incorporating lat/long into AC would still involve some modification to the traditional AC model. In comparison to the modification introduced here (local clustering), we viewed the direct tradeoff between geographic span and variance along other features as a conceptual defect of this model.

There are also ways that location data could be incorporated into clustering models other than the 'local clustering' algorithm introduced here.

There are additional areas of research apart from this suggestion for adding location data to the 'global clustering' algorithm. We briefly mention these in the following section.

Future steps

There are several further dimensions that can be explored in future work:

• The local method does have some disadvantages. It is more complex to tune and verify than the global version - it can be harder to know how to tune without geographic understanding, and it can be hard to verify the reasonableness of the clusters and anomalies without developing locally-applied variance metrics. Relatedly, dendrograms can't be used since the clustering algorithm is applied many times on the different map regions, and clusters may be glued together across map regions.
• The current grid representing lat/long coordinates is not dependent on features that one would consider useful, such as the house density in a particular area.  It would be more formally accurate to make it data-driven, and additional insights may result from such an implementation.  Some pairs of houses may be flagged as anomalies in the cities while only singletons would be flagged in the countryside, for example.   Given the new anomaly labels, we could once again conduct their analysis. The current implementation of the Kepler mapper does not support  a data-driven grid, instead relegating its creation to future work.
• To reiterate parts of the previous point, we implemented the mapper to construct the map regions in a very naive way - using the lat/long coordinates themselves. This was sufficient in this case, since Georgia is a relatively small region and is not close to the poles of the spherical coordinates. However, a more nuanced choice of map chunks, possibly guided by density and other data and/or surface area, may be necessary to scale the results appropriately.
• Current state of knowledge on the use of DBSCAN in geographic clustering recommends using latitude/longitude alone or only other features, not a mixture of both.  One would cluster on latitude/longitudes, for example, then apply other machine learning techniques to the resulting clusters.  While this is not a use case for anomaly detection, using an underlying grid of latitudes/longitudes and clustering other features using DBSCAN could be a promising use case for clustering on mixed data.
• Finally, the principal components are ranked in order of descending variance explained, yet the current machine learning algorithms that use them, including clustering, weigh them the same.  We would like to derive an approach that allows the relative importance of the principal components to be passed forward to other machine learning algorithms.

Conclusion

Our main task was to use alternative data to identify and characterize anomalies across a statewide single-family rental housing market. To accomplish this task, we developed a pipeline to bring in, clean, and create features from alternative data. This data had the benefit of being freely available, but was noisy or course-grained in many cases. We extracted useful signals from this data using via feature selection and engineering, scaling, principal component analysis, etc.

With the goal of performing stable clustering analyses, we ran the algorithms on the five principal components derived from the original features. Principal components 1 and 2 represented urban and suburban features, respectively. Principal components 3 and 4 were corrective components, respectively representing a tradeoff between a larger home vs. higher crime/worse schools, and better schools/suburban attractions/walkability vs. higher crime/decrease in posh features. Principal component 5 almost entirely identifies areas with high estimated average loss ratio to property.

We first applied traditional anomaly detection methods such as isolation forests and agglomerative clustering. Without further modifications, these methods detected statewide outliers, but failed to detect anomalies in many areas. In addition, traditional anomaly detection methods were overly swayed by outliers in the estimated average loss ratio.

To address the problem with local methods, we developed a localized agglomerative clustering technique. The key idea was to break up the dataset into overlapping 'rectangular' geographic regions by lat/long, run the agglomerative clustering on the principal components, and combine clusters containing a house in common until clusters are disjoint. This technique allowed clusters with larger intra-cluster variance than the global agglomerative clustering model, while still isolating the same number of listings. Our localized clustering method detected anomalies statewide and was less swayed by outliers in the estimated average loss ratio.

The localized agglomerative clustering technique allowed us to detect anomalies that are over $100K cheaper than houses in nearby clusters. The global anomaly detection methods failed to detect these anomalies, concentrating instead on properties that are likely to be of little interest to investors in single-family rental properties. While the localized agglomerative clustering technique is promising, we identified ways for improving it further. We identified other approaches to the localization problem, such as using the geographic information in the observation data itself. However, we leave these possibilities for future work.