Data Studying to Predict Iowa Housing Prices
The skills the author demoed here can be learned through taking Data Science with Machine Learning bootcamp with NYC Data Science Academy.
Introduction
The goal of this project was to utilize supervised machine learning techniques to predict housing prices in Ames, Iowa. The data set was provided by Kaggle, an online community of data scientists and machine learners, owned by Google.
My steps towards creating a highly accurate model were as follows:
- Data exploration and cleaning
- Feature engineering
- Modeling
- Aggregating the models built for additional accuracy
I. Data Exploration and Cleaning
The data set was split into a training dataset containing 1,460 sales and a test dataset with 1,419 sales. There were 80 variables, including the sale price, with 20 continuous, 14 discrete, 23 nominal, and 23 ordinal variables.
As sale price is the value I was looking to predict, it was also the first variable I examined. The sale price exhibited a right skewed distribution which was corrected by taking the log. A Box-Cox transformation was also applied, but the improvement, compared to simply applying a log transformation, was not significant.
After the log transform:
The next thing I noticed was the large amount of missing values for 34 different features (Sale Price shows NAs as I combined the test and train data sets):

Feature
The majority of the missing data corresponded to the absence of a feature. For example the Basement features, mentioned in the above table, showed up as "NA" if the house did not have a basement. These were imputed as 0 or "None" depending on the feature type. The remaining missing values fell into two types:
1) Categorical variables:
these were imputed after careful analysis of the relationship with Sale Price. For example, Kitchen Quality was imputed based on the sale price with the labels being: excellent (Ex) good (Gd), average (TA), or fair (Fa).

2) Numerical variables:
these were imputed via mean or median, whichever seemed most appropriate. The only numerical feature not imputed was Garage Year Built as it had a correlation coefficient of 0.84 with the year the house was built.
The final step before undertaking the feature engineering was to check for outliers. To do so I analyzed the most important indicators for sale price: Ground Living Area and Overall Quality. This allowed me to identify two outliers which were then eliminated from the data set:
II. Feature Engineering
Before creating or editing features, I first wanted to better understand the correlation amongst the variables of the housing data set. The heatmap below illustrates this structure. In this chart, darker colors indicate a larger correlation between two variables while lighter colors show a smaller correlation. The bottom row indicates the correlation between sale price and the various features included in the dataset. The correlation structure confirms the presumption that variables such as overall quality, age, and size being highly correlated with price.
This matrix of coefficients validated my thinking that certain features could be combined, entirely eliminated or re-engineered to extract additional meaning from the data while limiting noise. Here are the main modifications that I proceeded to do:
- Total Bathrooms: Sum of Above Ground Full, Half Baths, Basement Full and Half Bath.
- House Age: The difference between Year Sold and Year Remodeled
- Remodeled: Binary value that takes 1 if the house has a remodeled year that is different from the year it was built in
- Is New: Binary value that takes 1 if Year Sold equals Year Built
- Neighborhood Wealth: A categorical value (1-4) of different groups of houses based on disparities in their neighborhoods median wealth.
- TotalSF, Total Porch SF, and BsmtBath: sum of the square footage of their sub-features
- Exterior & Condition: Exterior1/2 and Condition1/2 were respectively combined
All re-engineered features were then analyzed to make sure they derived additional value compared to their predecessors. Below is the TotalSF feature which was the best re-engineered predictor of Sale Price:
III. Modeling Data
-
Linear Models:
Considering the large amount of features in this dataset, I decided not to build a basic multiple linear regression model and opted instead to start off with penalized regression models. All three models (Ridge, Lasso and Elastic Net) were built using cross-validation with 4 train folds and 1 test fold with each fold containing 20% of the train data. As expected, Lasso had a lower amount of variables kept as coefficients that are all progressively pushed to 0 as lambda tends towards infinity, and the elastic net model performed the best. However, the Ridge model ended up having the highest Kaggle score as seen below:
| Model | Specification | Variables Used | CV R^2 | CV RMSE | Kaggle Score |
| Ridge CV | Best Lambda: 0.035 | All | 0.9346 | 0.1238 | 0.1313 |
| Lasso CV | Best Lambda: | 72 | 0.9331 | 0.1207 | 0.1439 |
| Elastic Net CV | Best Alpha: 0.08
Best Lambda: 0.0163 |
81 | 0.9415 | 0.1179 | 0.1490 |
Below are the top-20 variables from the Ridge CV model. One should note that in general, the size of the coefficients is not necessarily an indication of importance. However, I have scaled all the variables for this chart, so one can directly infer the importance of these coefficients.

2. Tree-based models:
1) Random Forest: The reason why I included the Random Forest model is because it tends not to over-fit the training set, since each decision tree is limited to a number of factors. Although each individual decision tree might over-fit the data, all of the trees can be assembled to make a stronger predictor. This can be done because all of the individual trees are uncorrelated. As long as we have enough trees in the Random Forest, the 'noise' of each tree will be averaged out and the trend from the strong predictors will stand out.
Another benefit from this model is that it does not assume a linear relationship between the response and explanatory variables. However, one large disadvantage of this model is that its accuracy can heavily suffer when it is used for predicting based on data it has not seen before.
2) XGBoost: XGBoost produces extremely accurate models but can be prone to over-fitting, which contrasts well with Random Forest. The general methodology of boosting is that it creates a decision tree, and for every subsequent decision tree, it utilizes the residuals of that previous tree to make its prediction. As the number of trees in the boosting model is increased, the results become closer to their true value. This can lead to very accurate results but can generate strong over-fitting as the model's trees are correlated with each other.
I will not enumerate the multiple hyper and base parameters used for both of these models, but I have listed both of their RMSE scores on Kaggle:
Random Forest: 0.1311
XGBoost: 0.1202
Below is a graph of the importance of the XGBoost features. This feature list is actually quite similar to that of the Ridge CV model and maintains a rationalizable order.
IV. Aggregating the Models Built for Additional Accuracy
Having created the 5 models I wanted, I proceeded to use two different techniques to aggregate said models for more accurate predictions.
- Averaged Model: I combined all 5 models by assigning a unique weight to each model. The ideal weights that minimized RMSE were calculated using scipy.optimize.minimize.
- Stacked Model: Stacking highlights each of the 5 base models where they perform best and discredits them where they perform poorly. For this reason, stacking is most effective when the base models vary, hence my having done two different categories of models. To execute the stacking, I used the StackingCVRegressor, which works as depicted below:
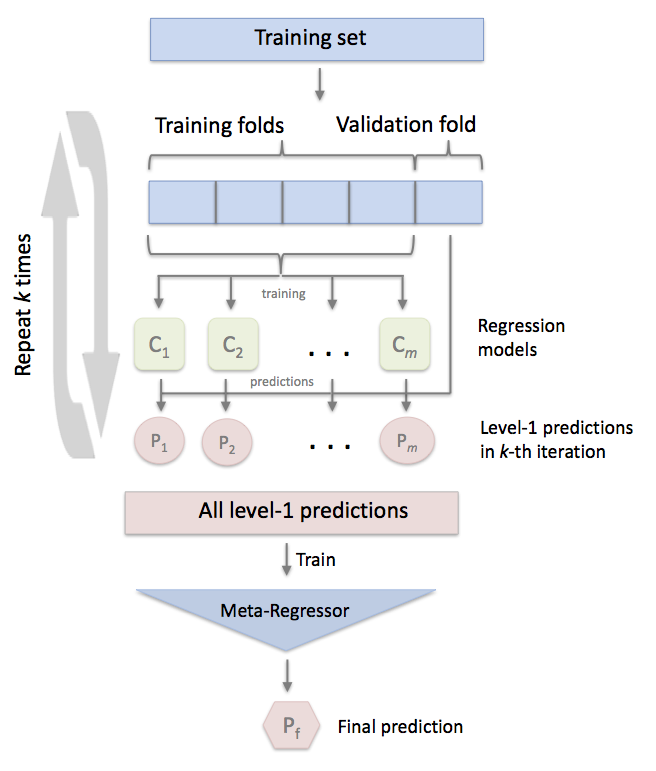
The user can choose which model is used as the "meta-regressor" for optimizing the stacked model. Of the 3 different models (SVM, Lasso and Random-Forest) I used for the meta regressor, Lasso performed the best, with a Kaggle score of 0.11544 which was my final submission!
Please feel free to reach out to me on LinkedIn if you have any questions or concerns, thanks!







