Using T-SVD to Study State Migration Data

In the project, we use the un-supervised learning method 'truncated singular value decomposition' to study the state to state annual population migration data, scraped from the IRS web site.

The Codes

The research in the project is done by using the python language. The web scraping is done using the popular web-scraping package 'beautiful soup'. We write a short object oriented python program to model the tree branching of the web links from the root and use a config file to control the behavior of the program. In this way, the program is agnostic to the web link structure, which makes it reusable if necessary.

The web-scrapping program can be found at Web Scraping Program

The config file can be found at The config file of the python program

The structure of the IRS state to state migration data is elegant. Unluckily the data is very dirty, due to the different formats of the excel files, the odd and high numbers of different abbreviations of the states and the changing file name conventions. So we have to write a python script to rectify that.

The script can be found at Data cleaning script

The script to convert the cleaned data into a python dictionary of the , using
the year strings as the keys Construct Migration Probability Matrices

The computation and plotting are done relying upon numpy, pandas, matplotlib and seaborn. We rely heavily on the wisdom of Horn's parallel analysis to simulate the random matrix singular values, as well as the distribution of covariance, correlation of the high dimensional residual noises. The computation are done using the various functions in SVD related computation

The script on plotting can be found at Plotting the Residuals, etc and 2D Heat Map and Top 20 Table

The Introduction to the state migration matrix

Every year law-abiding US residents file their federal returns with the IRS before the mid April deadline. They may not be aware that the IRS records and tracks their filing addresses or that they publish yearly statistics on migration patterns on their web site.

IRS logo

We collect the tax migration data through web scraping from IRS tax stats covering the year range 1990 to 2011. Approximately 2000 files were created for each year and merged together. What resulted was a 51x51 matrix (including Washington, DC). We need to normalize the data matrix appropriately because 1. More populated states would dominate and 2. Later years with higher population would dominate, creating bias.

While tracking migration patterns may seem simple on the face of it, it requires a sophisticated machine learning approach due to the nature of the data. As an example, a naive approach yields the following migration matrix.

The average yearly migration count. Without normalization, the large states California, New York and Florida are the focal points

The objective of the project is to apply machine learning technique to describe the behavior of US tax-payers' annual migration patterns. This will demonstrate the power of the truncated singular value decomposition (“T-SVD”) in helping to understand the migration data through dimension and noise reduction.

Instead of working with the raw migration data, we need to normalize the
annual migration matrices appropriately. We notice that the migration numbers often correlate positively with the state total population. The raw migration matrices tend to single out states like California, Texas, Florida... than the smaller states. It is well known that the population time series is not stationary (i.e. bounded within a fixed range). The per state populations in 1900 were much smaller than the current state populations in 2016. This suggests that the migration matrix time series could have a natural upward trend. To decouple the growth trend, we divide entries of the raw migration matrices by the averages of inbound and outbound annual non-migrant state return numbers. When state and state migration numbers are equal, the normalized ratios remain equal. The normalized numbers are far smaller than one, which warrants to be interpreted as the migration probabilities.

The sociologists have long noticed that in the old days, the American people often stayed in their hometown throughout their lifespan. This is not the case any more! The modernization of the society, fueled by the ease of long distance travel and a very dynamic economic evolution, often motivates people to leave their hometowns. Thus it is very meaningful to study the migration patterns, understanding the factors driving the long distance migration.

To provide the reader some general idea about the data we study, we present a 2D heat map of the time series average (between 1990-2011) migration probability matrix.

The time series average Migration Probability Matrix between 1990-2011, the values have been scaled up by 10000 to make the entries fall into the range (0,100).Otherwise the numbers are too small for human beings to comprehend

The migration probabilities are generally tiny, so we have to scale them up by 10,000, and the natural unit becomes 'bps'. We set their diagonal entries to zero in the above plot because the probabilities of staying in the same states are nearly one, and are not free parameters. If we include them into our time dependent migration probability matrices, [Latex]MM(t)[/Latex], all the off-diagonal entries become comparably insignificant. From now on, our convention is that all the reduced migration matrices have zeros on their diagonals.

It is probably very difficult to miss the white spot on the above heat map, which corresponds to a nearly 1% annual migration probability from D.C. to Maryland. As a matter of fact, the southern state border of Maryland half-surrounds D.C. and they share the same subway and transit system. This makes the migration from D.C. across the state border of Maryland so convenient, they are practically local moves. To demonstrate that this is not an isolated example, let us list the top 20 probabilities of (out of state, into state) pairs and display the result as a table,

The top 20 pairs of the migration probabilities

All of the top 20 migration state-to-state pairs consist of the states which border each other! While this does not surprise us, it exposes a serious obstacle to our analysis. The pairs (New York,New Jersey) and (Kansas, Missouri) are particularly suspicious. The super densely populated New York city is located near the border of New York state and New Jersey, while the Kansas city is at the Kansas and Missouri state border. So any NYC residents moving into Jersey city or any Kansas city residents changing their neighborhood would contribute to the state to state migration data.

The flooding of low-threshold semi-local moves in our data is exactly why the original migration probability matrices, though valuable, do not give us direct insights about why Americans give up their old residences and make long distance moves.

Luckily the un-supervised machine learning technique can help us to 'separate the wheat from the chaff'. In particular, we will use the truncated singular value decomposition, , to filter out the idiosyncratic 'noise' in our data.

In machine learning, it is often that one needs to factorize a large matrix into some matrix products. The matrix factorization technique has wide applications in the recommendation system, natural language processing (LSA/LSI, word2vec/CBOW....). The singular value decomposition, SVD, is unique under the umbrella term 'matrix factorization' in that it is essentially unique in the non-degenerated cases. Mathematically, it factorizes the square migration matrix MM into , where is diagonal, and are orthogonal matrices encoding the dependencies of the out-bound and in-bound states upon the various latent factors. (The non-square case can be factorized using SVD in the same manner by zero padding into a square matrix)

In a plot known as scree plot, we can plot the singular/eigen-values in their descending order,

The Singular Values of the time average Migration Matrix

Essentially the SVD of filters the matrix into different 'rank 1' layers and the individual singular value controls the significance of each layer. Depending on the user's conviction about the noisy nature of the matrix , one may keep only the top k (user chosen) singular values, known as choosing k latent factors, and interpret the sum of the remaining layers as noise. This procedure is known as the truncated singular value decomposition, T-SVD.

The random matrix theory, known as Horn's parallel analysis in this context, evaluates the information content of the matrix . The real art is to choose the number of factors, balancing the simplicity of the model and richness of its explanatory power. In our case, it suggests that it is safe to choose the top four (or slightly more) singular values above the background white noise. In our
analysis, we walk through the cases of 1, 4 and 7 latent factors.

One major defect of such naive approach is that the of with a varying k often do not approximate as a component-wise positive matrix. In other words, the negative entries can occur in the SVD approximations. It is very odd for a probability matrix to have negative coefficients! To remedy this, we have to convert by the log odd function, . After performing the T-SVD analysis, we convert the de-noised matrix into the original space by applying the well known sigmoid function (plotted below),

The sigmoid function widely used in neural network and logistic regression

Now we can formulate our time series , 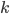latent-factor T-SVD by the following time series equations,

The latent factors and the annual migration matrices

In the following, we demonstrate how the varying k affects our state to state migration analysis.

For the single latent factor T-SVD, we assume there is a single hidden factor which affects Americans' migration. The model does not specify whether it is job-related, economically induced or not. The human needs to interpret according to the extracted factor. In such a single factor scenario, most of what we have seen in the original migration matrices are idiosyncratic noise. We have the following 2D heat map of the 'cleaned' time series average migration matrix.

1 latent factor T-SVD on the log odd time average MM, converting
back by the component-wise Sigmoid function transformation

By assuming only a single factor which affects American's moving decision, we get an extremely simplistic migration matrix, whose 2D heat map shows little similarity with the original migration matrix. Instead of using 51*(51-1)=2550 free parameters in describing the original migration matrix, the single latent factor version needs only 50+1+50=101 free parameters! The big surprise is that the highest probability migration route is NOT from D.C. to Maryland. Instead the Florida Colorado is the hottest route. This is the long distance move we are interested in. We display the top 20 migration routes in the following table.

The most popular migration routes after filtering by the single latent factor T-SVD

The major strength of SVD is that it analyzes the matrix data to extract the hidden patterns that the human eyes can not discern. It pulls out the most significant top k latent factors and brushes away the smaller corrections as noise. In the above table, it is surprising that most of the popular migration pairs are long distance moves, exactly what we like to pay more attention to in the migration pattern analysis.

Within them, the top out-bound states are Colorado, Florida, Virginia, Arizona, Texas, California, and South Carolina. The top in-bound states are Florida, Colorado, Arizona, Virginia, and Texas. All but
California and South Carolina are highly active in both the inbound and outbound migration routes. It seems that the warmer weather and economic strength influence people's migration decisions strongly.

To remedy the simplistic nature of the single latent factor T-SVD, we may relax our noise level cut-off and choose the k=4 or the higher k=7 T-SVD to approximate the migration probability matrices. For a given matrix, the k latent factor T-SVD approximation is the superposition of k different simplistic single latent factor (rank one) approximations (the mathematical advanced reader can refer to the appendix for an outline of this viewpoint).

For , we need 392 free parameters to approximate our . We have,

Choosing 4 latent factors in the T-SVD approximation

The top 20 state to state migration pairs for 4 latent factor T-SVD

The four latent factor approximation is more realistic and true to the original migration matrix, thanks to the richness of the 4-layer overlay. The top migration route is from New York state to Florida (rank 10th in the original ). The top out-bound states are New York, Iowa, Connecticut, Minnesota, Virginia, Wyoming, Montana, Massachusetts, New Jersey, Pennsylvania, North Carolina, Florida, Tennessee and Illinois. Florida remains both the in-bound/out-bound migration hot spot, which is not obvious from the original migration matrix.

The most popular in-bound states are Florida, Minnesota, Massachusetts, Iowa, Montana, Idaho, Wyoming, Connecticut, North Carolina, Georgia, Virginia and New York.

Unlike the single latent factor T-SVD approximation, both the low and high latitude states appear in this top list and quite a few of them are the original east coast 13 colonies.

for we have,

The sigmoid transformed 7 latent factor T-SVD approximation to the migration matrix

The top 20 state to state migration pairs for 7 latent factor T-SVD

The 7 latent factor T-SVD of the log odds migration probability matrix is an even better approximation to the original migration matrix than the 4 latent factor version. But the reader will definitely notice that most of the top migration routes are again neighbor states. Luckily the noise cut off is still enough to block away the the most problematic (Kansas,Missouri) pair and (New York,New Jersey) pair in the top list of the original migration matrix!

This example demonstrates that the choice of the number of latent factors is absolutely crucial for the purpose of noise reduction. The trade-off of simplicity of the low rank latent factor approximations and the goal to minimize the residual errors needs to strike a balance.

Our Conclusion

In this project, we kill two birds with one stone by achieving the dimension reduction and noise
reduction on the yearly state to state migration matrix time series using T-SVD. The technique allows us to drastically reduce the free parameters in the system and filter out the less important idiosyncratic adjacent state to state moves. To choose a good k, we need to balance out the simplicity of the model and the the low noise reduction capability for a large k. The range k \in [4,7] seems to be strike a balance. Due to the nonlinear nature of the sigmoid function, increasing k beyond 7 increases the root mean square error of the approximations using even more variables. This can be seen by the following heat map,

year vs number of latent factors RMSE heat map

The above 2D heat map indicates that the estimation error of the sigmoid transformed k latent factor T-SVD grows larger (color white) beyond k=8 and drops again only after k=35, throughout the year range 1990-2011. When k=35 it takes 2310 or more variables to describe such an annual migration matrix.

We have also analyzed the distribution residuals and find out that after adjusting for the degree of freedom, they do behave like white noise (i.e. normally distributed). But the different year's T-SVD residuals tend to have positive correlations, suggesting a temporal serial correlation not completely removable by the T-SVD technique. To our knowledge the residual noise
does behave like iid within the same year, but probably not the case for the full range of time series.

After this analysis was done we found out with some surprise that a similar type of sigmoid transformed matrix factorization structure appears in the research literatures of such hot topics as natural language processing and recommendation system design. This witnesses the power and versality of the same machine learning techniques to totally different types of applications.

If we turn the un-supervised machine learning question into a time series forecast (supervised machine learning) question on the yearly migration probability matrices, our analysis indicates that we probably need a recursive neural network structure to achieve dimension reduction and non-linear time series
forecast in one shot.

Appendix: Some explanation of the meaning of SVD

In this appendix, we offer the mathematical curious reader some simple linear algebraic computation to understand how does the singular value decomposition can be interpreted as the superposition of multiple
layers of rank-1 matrices, weighted by the descending singular values. This will make it more intuitive
to understand the effect of truncated SVD than the black box approach. Because our migration matrices
are all square (having the same row and column count), we restrict our discussion to the case of square matrices of size .

Suppose we have an SVD of the square matrix ,

with a diagonal , orthonormal .

We rewrite the matrices into the n column vectors in , and into the n row vectors in .

\begin{equation}
U=\begin{bmatrix}
{\bf u}_1 & {\bf u}_2 & \cdots & {\bf u}_n
\end{bmatrix}
\end{equation}
\begin{equation}
V=\begin{bmatrix}
{\bf v}_1^{T} \\
{\bf v}_2^{T} \\
\vdots \\
{\bf v}_n^{T}
\end{bmatrix}
\end{equation}

Suppose that the diagonal entries of the diagonal matrix are , it is not hard to see that the matrix product is nothing but

\begin{equation}
\tilde{U}=U\Lambda = \begin{bmatrix}
\lambda_1{\bf u}_1 & \lambda_2{\bf u}_2 & \cdots & \lambda_n{\bf u}_n
\end{bmatrix}
\end{equation}

Thus is equal to

\begin{equation}
\begin{bmatrix}
\lambda_1{\bf u}_1 & \lambda_2{\bf u}_2 & \cdots & \lambda_n{\bf u}_n
\end{bmatrix}
\begin{bmatrix}
{\bf v}_1^{T} \\
{\bf v}_2^{T} \\
\vdots \\
{\bf v}_n^{T}
\end{bmatrix}
\end{equation}

If are not vectors but are merely real numbers, the above matrix product is nothing but the usual dot product of two n dimensional vectors and we can multiply happily using the matrix row to column multiplication to get . Even when all are n dimensional vectors in , we can still make sense of . Because a column vector is in effect an n by 1 matrix, and a row vector is in effect an 1 by n matrix, the matrix product is an matrix.

Thus the above representation of the matrix product suggests an linear expansion,

\begin{equation}U\cdot \Lambda \cdot V
= \lambda_1 {\bf u}_1{\bf v}_1^{T}+\lambda_2{\bf u}_2{\bf v}_2^{T}+\cdots \lambda_n{\bf u}_n{\bf v}_n^{T}
\end{equation},

which can be proved rigorously. This is the expression which makes the mechanism of the SVD or T-SVD most transparant. The product , usually called a rank-1 update, can be expressed as , the tensor product of the n-component .

So our SVD decomposition can be written succinctly as

\begin{equation}
U\cdot \Lambda \cdot V
= \lambda_1 {\bf u}_1\otimes {\bf v}_1+\lambda_2{\bf u}_2\otimes {\bf v}_2+\cdots \lambda_n {\bf u}_n\otimes{\bf v}_n
\end{equation}.

Before we interpret this expansion of products here, we give a simple example of .

Let and , then is equal to

\begin{equation}
\begin{bmatrix}
1 & -1 & 3 \\
2 & -2 & 6 \\
4 & -4 & 12
\end{bmatrix}
\end{equation}

The matrix displays patterns among the columns and rows not seen on the generic matrices. This is exactly what SVD is searching for in its pattern recognition task.
If move freely in , the tensor product have 6 free parameters. But a generic matrix has 9 free parameters. This observation tells us that the matrix of the form are rather degenerated in the space of matrices. These special matrices are of rank 1, while the generic matrices are of rank 3. The SVD of an matrix decomposes it into the sum of rank 1 matrices, with the additional property that are orthonormal. So are the . By orthogonality on , we mean

\begin{equation}
{\bf u}_i\cdot {\bf u}_i = 1, 1\leq i\leq n; {\bf u}_i\cdot {\bf u}_j=0, 1\leq i\neq j\leq n
\end{equation}.

Finally, we offer a simple interpretation of the SVD. The 2D heat map allows us to plot the values
of a migration probability matrix by encoding them as the color spectrum. This illustrates the fact that any square matrix A can be viewed as an function from the 2D lattice grid into . Similarly, a vector having n components can be viewed as function from a 1 dimensional lattice grid of n points into .

Mathematically we can express these as the functions , and , respectively.

Thus, the SVD simply means that the 'function' A living on the 2D lattice grid can be expanded into the sum of n 'monomials', with each of the 'monomial' being the product of two functions living on the 1D lattice grids. All these 1D lattice grid functions are mutually perpendicular to each other, with the lengths being one.

Have we seen this phenomenon before? Imagine that the n increases indefinitely to , the 2D-lattice grid approaches the the unit square, the 1D-lattice grid approaches the unit interval, following the spirit of Calculus using finer and finer grids to approach continuity. In the continuity limit, what does the SVD-like expansion mean?

In such a limit, the original A can be viewed as , and the SVD-like expansion would look like

\begin{equation}
{\bf K}(x,y) = c_1{\boldsymbol\phi}_1(x){\boldsymbol \psi}_1(y)+c_2{\boldsymbol\phi}_2(x){\boldsymbol\psi}_2(y)+c_3{ \boldsymbol\phi}_3(x){\boldsymbol \psi}_3(y)\cdots,
\end{equation}

while the discrete orthogonality conditions on the vectors are replaced by the integrals,

\begin{equation}
\langle {\boldsymbol\phi}_i,{ \boldsymbol\phi}_j\rangle = \int_{-1}^{1} {\boldsymbol \phi}_i(x){\boldsymbol \phi}_j(x) dx = 0; 1\leq i\neq j \leq \infty.
\end{equation}

For example, if we consider the anti-symmetric kernel function , the reader probably had learned in the high school trigonometry course that it can be expanded into

\begin{equation}
{\bf sin}(2\pi(x-y)) = {\bf sin}(2\pi x){\bf cos}(2\pi y)-{\bf cos}(2\pi x){\bf sin}(2\pi y).
\end{equation}

In this simple example, ,, with the orthogonal relationship,

\begin{equation}
\langle {\bf cos}(2\pi x), {\bf sin}(2\pi x)\rangle = \int_0^1{\bf cos}(2\pi x){\bf sin}(2\pi x) dx = 0,
\end{equation}

fundamental in the theory of Fourier series/analysis.

Summary

We end the appendix by summarising that SVD filters the matrix A into multi-layers of simple rank 1 matrices, sorted by the descending order of the coefficients, called the singular values. Each of them offers a very simplistic approximation of the original matrix, but the overlay of the dominated layers provide a better approximation of the original matrix. In the limit we take in all the singular values, the approximation to the original matrix becomes perfect, but we are using no less than degree of freedom to capture the full information on A. So we must strike a balance to minimize the number of parameters and to seek a smaller approximation error to our data.

In the large n limit, the SVD decomposition is tied to the kernel function expansion. In the special case of the symmetric kernel, SVD is reduced to its cousin algorithm PCA and the kernel expansion is nothing but the kernel function diagonalization fundamental to the theory of another machine learning algorithm 'support vector machine'.