Credit Card Fraud Detection
Introduction
One of the major pain points for the credit card industry has been to accurately find potential fraudulent transactions and to process them to completion. Every credit card transaction that requires the involvement of a customer service representative costs the company money. Credit card is often a payment method of convenience for the user. The more the genuine transactions get delayed due to checks in place to prevent fraud, the greater is the chance to alienate the consumer. Similarly, credit card firms will need to built a larger customer service workforce to ensure timely processing of transactions.
About the data
The data that has been used as part of this project is from kaggle. Quoting from kaggle, “The datasets contains transactions made by credit cards in September 2013 by european cardholders. This dataset presents transactions that occurred in two days, where we have 492 frauds out of 284,807 transactions. The dataset is highly unbalanced, the positive class (frauds) account for 0.172% of all transactions.
It contains only numerical input variables which are the result of a PCA transformation. Unfortunately, due to confidentiality issues, we cannot provide the original features and more background information about the data. Features V1, V2, … V28 are the principal components obtained with PCA, the only features which have not been transformed with PCA are ‘Time’ and ‘Amount’. Feature ‘Time’ contains the seconds elapsed between each transaction and the first transaction in the dataset. The feature ‘Amount’ is the transaction Amount, this feature can be used for example-dependant cost-senstive learning. Feature ‘Class’ is the response variable and it takes value 1 in case of fraud and 0 otherwise.
Given the class imbalance ratio, we recommend measuring the accuracy using the Area Under the Precision-Recall Curve (AUPRC). Confusion matrix accuracy is not meaningful for unbalanced classification.
The dataset has been collected and analysed during a research collaboration of Worldline and the Machine Learning Group (http://mlg.ulb.ac.be) of ULB (Université Libre de Bruxelles) on big data mining and fraud detection. More details on current and past projects on related topics are available on http://mlg.ulb.ac.be/BruFence and http://mlg.ulb.ac.be/ARTML
Please cite: Andrea Dal Pozzolo, Olivier Caelen, Reid A. Johnson and Gianluca Bontempi. Calibrating Probability with Undersampling for Unbalanced Classification. In Symposium on Computational Intelligence and Data Mining (CIDM), IEEE, 2015 "
Loading the data
The Class Column contains 0 or 1 and these numerical levels are converter to a column with two levels. Genuine or Fraud
ccfraud <- read.csv('creditcard.csv'))
ccfraud$Class <- as.factor(ccfraud$Class)
levels(ccfraud$Class) <- c("Genuine", "Fraud"
Inspecting the data, we can confirm that there are 492 fraudulent transactions in our data file.
dim(ccfraud)
## [1] 284807 31
ftable(ccfraud$Class)Genuine Fraud ## ## 284315 492
The Mice package was used to inspect if we have any missing values. There were none.
data(ccfraud, package = "VIM")
## Show incomplete cases
sleep[!complete.cases(ccfraud),]
library(mice)
#md.pattern(ccfraud)
There are no missing data in the dataset. ## Plots on each of the variables
cn <- colnames(ccfraud[,1:30])
print(cn
)## [1] "Time" "V1" "V2" "V3" "V4" "V5" "V6"
## [8] "V7" "V8" "V9" "V10" "V11" "V12" "V13"
## [15] "V14" "V15" "V16" "V17" "V18" "V19" "V20"
## [22] "V21" "V22" "V23" "V24" "V25" "V26" "V27"
## [29] "V28" "Amount"
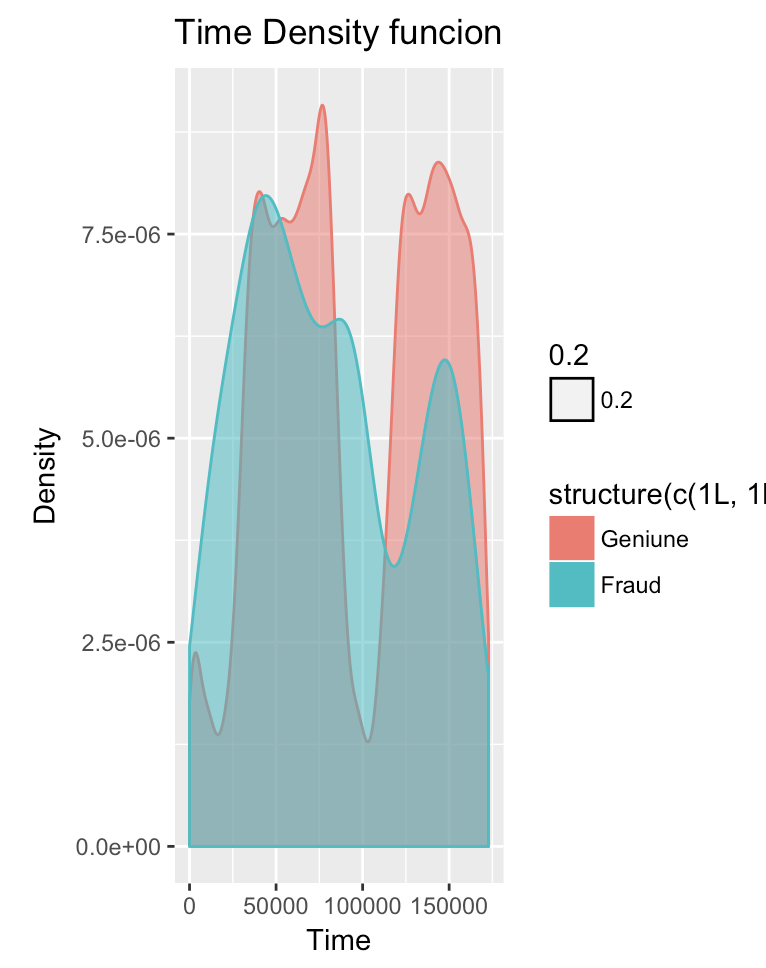
vars = paste("V", 1:30, sep="") par(mfrow=c(29,4)) library(ggplot2) for( var in cn){ p <- ggplot(ccfraud, aes_string(x = var, fill = ccfraud$Class, colour = ccfraud$Class, alpha = 0.2)) + geom_density() + xlab(paste(var)) + ylab("Density") + ggtitle(paste(var, "Density funcion")) print(p) }
## Correlation Plot This is not really important here as input data is already a PCA tranformation.
library(corrplot) cp <- corrplot(cor(ccfraud[, 1:30]))
Class Imbalance and approaches to solve it
The data set featured is one that has a highly unbalanced set of data with regards to the class type. 284315 genuine records vs 437 fraudulent ones. In case of unbalanced data, its better to look at precision and recall values to determine if the model is good. Also, from a business stand point, the more the false positives, the more the effort required by customer service to clear it and more the false negatives, more is the danger of losing money due to fraudulent transactions.
There are couple of approaches to solve class imbalance and train a model correctly. We will try various approaches and will see if it helps us to generate a good model.
- Class Weights
- Up Sampling
- Down Sampling
- SMOTE(Synthetic Minority Sampling Technique)
Splitting Data for our train/test
library(caret)## Loading required package: latticeset.seed(123)
index <- createDataPartition(ccfraud$Class, p = 0.7, list = FALSE)
train_data <- ccfraud[index, ]
test_data <- ccfraud[-index, ]
ftable(train_data$Class)## Genuine Fraud
##
## 199021 345ftable(test_data$Class)## Genuine Fraud
##
## 85294 147MiscFactors <- c()
pcafactors <-paste("V", 1:28, sep="")
formula = reformulate(termlabels = c(MiscFactors,pcafactors), response = 'Class')
print (formula)## Class ~ V1 + V2 + V3 + V4 + V5 + V6 + V7 + V8 + V9 + V10 + V11 +
## V12 + V13 + V14 + V15 + V16 + V17 + V18 + V19 + V20 + V21 +
## V22 + V23 + V24 + V25 + V26 + V27 + V28ControlParamteres <- trainControl(method = "cv",
number = 10,
savePredictions = TRUE,
classProbs = TRUE,
verboseIter = TRUE
)
str(train_data)## 'data.frame': 199366 obs. of 31 variables:
## $ Time : num 0 0 1 1 2 2 4 7 7 10 ...
## $ V1 : num -1.36 1.192 -1.358 -0.966 -1.158 ...
## $ V2 : num -0.0728 0.2662 -1.3402 -0.1852 0.8777 ...
## $ V3 : num 2.536 0.166 1.773 1.793 1.549 ...
## $ V4 : num 1.378 0.448 0.38 -0.863 0.403 ...
## $ V5 : num -0.3383 0.06 -0.5032 -0.0103 -0.4072 ...
## $ V6 : num 0.4624 -0.0824 1.8005 1.2472 0.0959 ...
## $ V7 : num 0.2396 -0.0788 0.7915 0.2376 0.5929 ...
## $ V8 : num 0.0987 0.0851 0.2477 0.3774 -0.2705 ...
## $ V9 : num 0.364 -0.255 -1.515 -1.387 0.818 ...
## $ V10 : num 0.0908 -0.167 0.2076 -0.055 0.7531 ...
## $ V11 : num -0.552 1.613 0.625 -0.226 -0.823 ...
## $ V12 : num -0.6178 1.0652 0.0661 0.1782 0.5382 ...
## $ V13 : num -0.991 0.489 0.717 0.508 1.346 ...
## $ V14 : num -0.311 -0.144 -0.166 -0.288 -1.12 ...
## $ V15 : num 1.468 0.636 2.346 -0.631 0.175 ...
## $ V16 : num -0.47 0.464 -2.89 -1.06 -0.451 ...
## $ V17 : num 0.208 -0.115 1.11 -0.684 -0.237 ...
## $ V18 : num 0.0258 -0.1834 -0.1214 1.9658 -0.0382 ...
## $ V19 : num 0.404 -0.146 -2.262 -1.233 0.803 ...
## $ V20 : num 0.2514 -0.0691 0.525 -0.208 0.4085 ...
## $ V21 : num -0.01831 -0.22578 0.248 -0.1083 -0.00943 ...
## $ V22 : num 0.27784 -0.63867 0.77168 0.00527 0.79828 ...
## $ V23 : num -0.11 0.101 0.909 -0.19 -0.137 ...
## $ V24 : num 0.0669 -0.3398 -0.6893 -1.1756 0.1413 ...
## $ V25 : num 0.129 0.167 -0.328 0.647 -0.206 ...
## $ V26 : num -0.189 0.126 -0.139 -0.222 0.502 ...
## $ V27 : num 0.13356 -0.00898 -0.05535 0.06272 0.21942 ...
## $ V28 : num -0.0211 0.0147 -0.0598 0.0615 0.2152 ...
## $ Amount: num 149.62 2.69 378.66 123.5 69.99 ...
## $ Class : Factor w/ 2 levels "Genuine","Fraud": 1 1 1 1 1 1 1 1 1 1 ...model.glm <- train(formula, data = train_data,method = "glm", family="binomial", trControl = ControlParamteres)## + Fold01: parameter=none
## - Fold01: parameter=none
## + Fold02: parameter=none
## - Fold02: parameter=none
## + Fold03: parameter=none## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred## - Fold03: parameter=none
## + Fold04: parameter=none
## - Fold04: parameter=none
## + Fold05: parameter=none
## - Fold05: parameter=none
## + Fold06: parameter=none
## - Fold06: parameter=none
## + Fold07: parameter=none
## - Fold07: parameter=none
## + Fold08: parameter=none
## - Fold08: parameter=none
## + Fold09: parameter=none
## - Fold09: parameter=none
## + Fold10: parameter=none
## - Fold10: parameter=none
## Aggregating results
## Fitting final model on full training setexp(coef(model.glm$finalModel))## (Intercept) V1 V2 V3 V4
## 0.0001958784 1.0465226361 0.9692444177 1.0153588236 1.9545622788
## V5 V6 V7 V8 V9
## 1.0040275509 0.8729683757 0.9622179694 0.8190839236 0.8090811225
## V10 V11 V12 V13 V14
## 0.4658158788 1.0298687876 0.9696172856 0.7447382118 0.5935635399
## V15 V16 V17 V18 V19
## 0.9115946086 0.8742182886 1.0436825514 0.9773124043 1.0100473879
## V20 V21 V22 V23 V24
## 0.7444748231 1.4329545639 1.5347401880 0.8957445857 0.9727523021
## V25 V26 V27 V28
## 0.8206291918 1.1151834700 0.5184477350 0.7885349948Making Predictions
pred <- predict(model.glm, newdata=test_data)
accuracy <- table(pred, test_data[,"Class"])
sum(diag(accuracy))/sum(accuracy)## [1] 0.9990754pred = predict(model.glm, newdata=test_data)
confusionMatrix(data=pred, test_data$Class)## Confusion Matrix and Statistics
##
## Reference
## Prediction Genuine Fraud
## Genuine 85272 57
## Fraud 22 90
##
## Accuracy : 0.9991
## 95% CI : (0.9988, 0.9993)
## No Information Rate : 0.9983
## P-Value [Acc > NIR] : 5.509e-10
##
## Kappa : 0.6945
## Mcnemar's Test P-Value : 0.0001306
##
## Sensitivity : 0.9997
## Specificity : 0.6122
## Pos Pred Value : 0.9993
## Neg Pred Value : 0.8036
## Prevalence : 0.9983
## Detection Rate : 0.9980
## Detection Prevalence : 0.9987
## Balanced Accuracy : 0.8060
##
## 'Positive' Class : Genuine
##
The gradient Boosting model.
MiscFactors <- c()
pcafactors <-paste("V", 1:28, sep="")
formula = reformulate(termlabels = c(MiscFactors,pcafactors), response = 'Class')
print (formula)
ControlParamteres <- trainControl(method = "cv",
number = 10,
savePredictions = TRUE,
classProbs = TRUE,
verboseIter = TRUE
)
str(train_data)
model.gbm <- train(formula, data = train_data,method = "gbm", metric ="ROC", trControl = ControlParamteres)
#exp(coef(model.gbm$finalModel))
summary(model.gbm)
print(model.gbm)
Stochastic Gradient Boosting
199366 samples
28 predictor
2 classes: 'Geniune', 'Fraud'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 179429, 179429, 179429, 179430, 179430, 179430, ...
Resampling results across tuning parameters:
interaction.depth n.trees Accuracy Kappa
1 50 0.9983147 0.1565414
1 100 0.9983147 0.1565414
1 150 0.9983147 0.1565414
2 50 0.9983748 0.1829052
2 100 0.9984049 0.2482535
2 150 0.9984701 0.2647271
3 50 0.9985855 0.3733709
3 100 0.8990520 0.3826216
3 150 0.8990369 0.4040990
Tuning parameter 'shrinkage' was held constant at a value of 0.1
Tuning
parameter 'n.minobsinnode' was held constant at a value of 10
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were n.trees = 50, interaction.depth = 3, shrinkage = 0.1
and n.minobsinnode = 10.
Making Predictions using GBM
pred <- predict(model.gbm, newdata=test_data)
accuracy <- table(pred, test_data[,"Class"])
print(accuracy)
sum(diag(accuracy))/sum(accuracy)
confusionMatrix(data=pred, test_data$Class)
Confusion Matrix and Statistics
Reference
Prediction Geniune Fraud
Geniune 85284 128
Fraud 10 19
Accuracy : 0.9984
95% CI : (0.9981, 0.9986)
No Information Rate : 0.9983
P-Value [Acc > NIR] : 0.2436
Kappa : 0.2155
Mcnemar's Test P-Value : <2e-16
Sensitivity : 0.9999
Specificity : 0.1293
Pos Pred Value : 0.9985
Neg Pred Value : 0.6552
Prevalence : 0.9983
Detection Rate : 0.9982
Detection Prevalence : 0.9997
Balanced Accuracy : 0.5646
'Positive' Class : Geniune
Making Predictions using Random Forest
mtry <- sqrt(ncol(train_data))
tuneGrid=expand.grid(.mtry=mtry)
ControlParamteres <- trainControl(method = "cv",
number = 10,
savePredictions = TRUE,
classProbs = TRUE,
verboseIter = TRUE
)model.rf <- train(formula, data = train_data,method = "rf", family="binomial", metric="Accuracy", trControl = ControlParamteres, tuneGrid=tuneGrid)pred <- predict(model.rf, newdata=test_data)
accuracy <- table(pred, test_data[,"Class"])
print(accuracy)##
## pred Geniune Fraud
## Geniune 85289 28
## Fraud 5 119Making Predictions using Naive Bias
x=train_data[, -c(1,31)] # Removing Time and Class
y=train_data$Class
names(x)
grid <- data.frame(fL=c(0,0.5,1.0), usekernel = TRUE, adjust=c(0,0.5,1.0))
model = train(x,y,'nb',trControl=trainControl(method='cv',number=10),tuneGrid=grid)
model
prediction <- predict(model$finalModel,x)
table(prediction$class,y)
naive_ccfraud <- NaiveBayes(ccfraud$Class ~ ., data = ccfraud)
plot(naive_ccfraud)
x=test_data[, -c(1,31)] # Removing Time and Class
y=test_data$Class
prediction <- predict(model$finalModel,x)
table(prediction$class,y)
## Naive Bayes
##
## 199366 samples
## 29 predictor
## 2 classes: '0', '1'
##
## No pre-processing
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 179430, 179430, 179429, 179429, 179429, 179429, ...
## Resampling results across tuning parameters:
##
## fL adjust Accuracy Kappa
## 0.0 0.0 NaN NaN
## 0.5 0.5 0.9978131 0.5481458
## 1.0 1.0 0.9957515 0.3954902
##
## Tuning parameter 'usekernel' was held constant at a value of TRUE
## Accuracy was used to select the optimal model using the largest value.
## The final values used for the model were fL = 0.5, usekernel = TRUE
## and adjust = 0.5.## y
## 0 1
## 0 198799 75
## 1 222 270| GLM | GBM | Random Forest | ||||
| Geniune | 85272 |
57 |
85284 |
128 |
85289 |
28 |
| Fraud | 22 |
90 |
10 |
19 |
5 |
119 |
## pred Geniune Fraud
## Geniune 85289 28
## Fraud 5 119